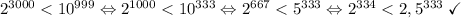98 ! заранее !
а). представьте число 100 в виде суммы нескольких натуральных чисел так, чтобы их произведение было наибольшим. и докажите, что большее произведение получить нельзя.
б). перемножили три тысячи двоек. докажите, что в записи получившегося числа:
не более 1000 цифр и не менее 900 цифр.
Другие вопросы по теме Математика
Популярные вопросы
- Два проводника одинаковой длины из одного и того же материала соединены последовательно....
2 - Чому дорівнює значення виразу √2*√14: √7?...
3 - Сочинение 6класс по плану как красива природа зимой план: 1небо 2воздух 3все...
1 - Rewrite the complete sentence using the adverb of frequency in brackets in its...
1 - С. нужно.заранее огромное ) 2. укажите даты событий. 1)протекторат кромвеля 2)реставрация...
2 - Через яку точку проходить графік рівняння 4у-3х=5? потрібне розвязання...
3 - Человек выполняет работу за 14 дней. если он будет работать вместе с сыном, то...
1 - Нужно к двум предложениям задать вопросы (общий; специальный; альтернативный...
3 - Высолов регистрации международного аэропорта домодедово тоже меня сеня 200.100...
1 - Кбезусловным пищ. рефлексам относиться 1)выделние слюны в ответ на звонок с занятия...
1
а)Пусть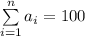 , при этом
, при этом 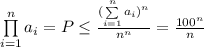 ; Пусть
; Пусть 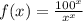 , тогда
, тогда 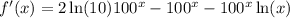 ; Экстремум находится в точке
; Экстремум находится в точке 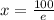 ;
; 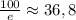 ; Поэтому при
; Поэтому при 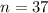 достигается максимум, т.е. 100 должно быть представлено в виде 37-ми слагаемых. А, значит, каждое из слагаемых либо 3, либо 2. Значит, искомое произведение есть число вида
достигается максимум, т.е. 100 должно быть представлено в виде 37-ми слагаемых. А, значит, каждое из слагаемых либо 3, либо 2. Значит, искомое произведение есть число вида  .
.  , поэтому чем больше m, тем лучше (возраст. функция). Стало быть, m=32, а искомый набор:
, поэтому чем больше m, тем лучше (возраст. функция). Стало быть, m=32, а искомый набор: 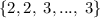 - 32 тройки и две двойки.
- 32 тройки и две двойки.
б) Нужно доказать неравенства: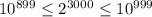
Покажем справедливость первого:
Теперь второго: