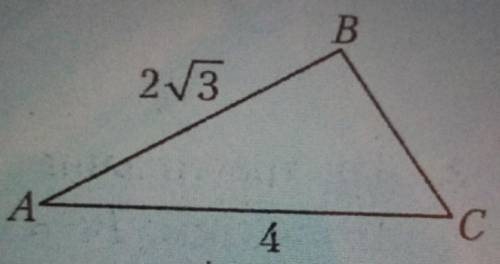
3. Дан треугольник ABC (рис.3),AB = 2√3 см, AC = 4 см, синусострого угла A равен 0,5. Найдите Равс​

6 + 2√3

Пошаговое объяснение:

1) Площадь треугольника равна половине произведения его сторон на синус угла между ними:

S авс = (АВ · АС · sin∠А) : 2 = 2√3 · 4 · 0,5 : 2 = 2√3

2) С другой стороны, площадь ΔАВС равна половине произведения основания АС на высоту, опущенную из вершины В на сторону АС (назовём эту высоту ВF):

S авс = АС · BF : 2

Подставим вместо S авс её значение и найдём BF:  

2√3 = АС · BF : 2

2√3 = 4 · BF : 2

BF = 2√3 : 2 = √3

3) Зная BF, найдём АF и FC.

AF = √(АВ² - BF²) = √((2√3)² - (√3)²) = √(4·3 - 3) = √9 = 3 см

FC = АС - АF = 4 - 3 = 1 см  

4) Зная FC, найдём ВС по теореме Пифагора, т.к. Δ BFC - прямоугольный:

ВС = √(BF² + FC²) = √((√3)² + 1²) = √(3+1) = 2

5) Равс = ​АВ + ВС + АС = 2√3 + 2 + 4 = 6 + 2√3 = 2· (3 +√3)

Для начала, давайте вспомним определение синуса острого угла в прямоугольном треугольнике. Синус угла определяется отношением противолежащего катета к гипотенузе треугольника.

В данной задаче у нас уже известны значения двух сторон треугольника, AB и AC, равные 2√3 см и 4 см соответственно, и значение синуса угла A, равное 0,5. Нам нужно найти значение угла A.

Для решения задачи мы можем воспользоваться формулой синуса. Формула синуса в треугольнике ABC выглядит следующим образом:

sin(A) = противолежащий катет / гипотенуза = AB / AC

Подставляя известные значения, получаем:

0,5 = 2√3 см / 4 см

Для упрощения выражения мы можем сократить общий множитель 2 в числителе и знаменателе:

0,5 = √3 см / 2 см

Теперь мы можем избавиться от знаменателя 2, умножив обе части равенства на 2:

0,5 * 2 = √3 см

Избавляясь от знака корня, получаем:

1 = √3 см

Теперь возведем обе части равенства в квадрат, чтобы избавиться от знака корня:

1^2 = (√3)^2

1 = 3 см^2

Таким образом, мы получаем неверное равенство, поскольку 1 не равно 3. Возникает противоречие, что означает, что исходные данные задачи некорректны. Какая-то ошибка была допущена в условии задачи или в данных.

Рекомендуется обратиться к преподавателю или автору задачи, чтобы уточнить данные или исправить ошибку.