(00-9-55) Найдите область значений функции y=√x²-x
с объяснением

Область значений функции [ 0; +∞)

Пошаговое объяснение:

Найти область значений функции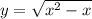  

Найдем область определения данной функции

Так как арифметический квадратный корень определен на множестве неотрицательных чисел, то найдем область определения заданной функции, решив неравенство:

x=0  или  x=1

Точки 0 и 1 разбивают числовую прямую на три промежутка. Определим знак на каждом промежутке ( во вложении)

Получим, что х ∈ (- ∞; 0]∪ [1; + ∞)

Тогда область определения D(y) =(- ∞; 0]∪ [1; + ∞)

Построим на полученной области определения график заданной функции ( график во вложении)

Область значений функции - это множество значений , принимаемых переменной y.

По графику определяем, что

y ∈ [0; + ∞)

Значит, область значений функции [ 0; +∞)