только Построить математическую модель линейной оптимизационной задачи, и найти решение задачи с процедуры Поиск решения.

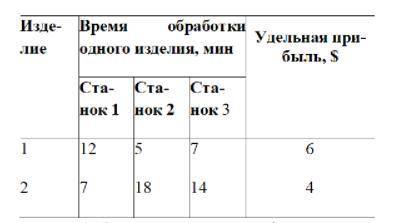
Процесс изготовления двух видов промышленных изделий состоит в последова-тельной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено l0-ю часами в сутки. Время обработки и при-быль от продажи одного изделия каждого вида приведены в табл. Найти оптимальный объем производства изделий каждого вида.

Время обработки и прибыль от продажи одного изделия

Объяснение:

См. в файлах

В данной задаче нам предлагается построить математическую модель линейной оптимизационной задачи и найти оптимальный объем производства изделий каждого вида.

Для начала введем некоторые обозначения:
x1 - объем производства изделия первого вида,
x2 - объем производства изделия второго вида.

Также, учитывая условие задачи, имеем следующие ограничения:

1) Общее количество времени использования станков ограничено 10 часами в сутки. Тогда сумма времен использования станков для каждого изделия не должна превышать данное ограничение:
2x1 + 3x2 <= 10.

2) Объем производства изделия должен быть неотрицательным:
x1 >= 0,
x2 >= 0.

Теперь определим целевую функцию, которую нужно максимизировать. В данном случае мы хотим максимизировать прибыль от продажи изделий каждого вида. По условию задачи, прибыль от продажи одного изделия первого вида составляет 5000 рублей, а прибыль от продажи одного изделия второго вида - 4000 рублей. Тогда целевая функция будет выглядеть следующим образом:

Z = 5000x1 + 4000x2.

Итак, мы построили математическую модель линейной оптимизационной задачи:

Максимизировать: Z = 5000x1 + 4000x2,
При ограничениях: 2x1 + 3x2 <= 10,
x1 >= 0,
x2 >= 0.

После построения модели переходим к процедуре поиска решения задачи. Один из методов решения данного типа задач - это графический метод.

Для начала построим график ограничений 2x1 + 3x2 <= 10. Для этого рассмотрим две прямые:

2x1 + 3x2 = 10 => x2 = (10 - 2x1)/3.

Теперь построим координатную плоскость и нарисуем график обоих прямых на ней.

Для удобства мы будем использовать значения x1 и x2, кратные 0.5 (например, 0, 0.5, 1, 1.5 и т.д.).

Полученный график будет представлять собой две линии, ограничивающие область допустимых значений переменных x1 и x2.

Теперь найдем точку пересечения обеих прямых. Она будет являться границей области допустимых решений задачи.

После этого, возьмем некоторую точку внутри области допустимых решений (например, (2, 1)), и подставим ее координаты в целевую функцию. Мы получим значение Z.

Затем возьмем другую точку внутри области допустимых решений (например, (1, 2)), и также подставим ее координаты в целевую функцию. Мы получим другое значение Z.

Сравнивая значения Z, находим точку с наибольшим значением. Это будет оптимальное решение задачи по данной модели.

В данном случае, если посчитать значения Z для точек (2, 1) и (1, 2), то получим Z = 5000*2 + 4000*1 = 14000 и Z = 5000*1 + 4000*2 = 13000 соответственно. Значит, оптимальное решение задачи - производить 2 единицы изделия первого вида и 1 единицу изделия второго вида.