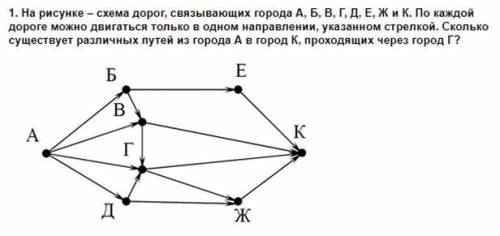
На рисунке - схема дорог, связывающих города А, Б, В, Г, Д. Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город Г РИСУНОК ПРИКРЕПИЛА
Другие вопросы по теме Информатика
Популярные вопросы
- Знайти найбільше значення виразу х/у,якщо х^2-7xу=18у^2...
2 - Варифмитической прогрессии а1= -8, а разность прогремит d=3....
2 - )спишите слова, раскрывая скобки и распределяя их по группам:...
3 - Хорошо в осеннем цветистом лесу синтаксический разбор...
1 - Решите неравенство √30-x-x² -1 ( выражение 30-x-x² полностью...
1 - Написать изложение 70 слов до завтра, завтра экзамен серпилин....
1 - Найти градусную меру большего угла равнобедреной трапеции авс...
2 - Учеловека гемофилия — сцепленный с х–хромосомой рецессивный признак....
2 - Найдите производную функции f(x)=(2x-1)^3...
2 - С! у меня получается 15, а в ответе 20. не понимаю, почему. заранее...
1
Чтобы найти количество путей из А в К через Г, нам нужно выбрать путь от А до Г и путь от Г до К. Поскольку мы можем перемещаться только в одном направлении, сначала мы должны выбрать путь, который ведет от А до Г, а затем выбрать путь от Г до К.
Мы можем обозначить количество путей от А до Г через букву N, а количество путей от Г до К через букву M. Тогда общее количество путей от А до К через Г будет равно произведению N и M.
Для нахождения N (количество путей от А до Г) мы можем использовать следующий подход. Из города А можем пойти только в городы Б и В. Из города Б можем пойти только в городы В и Г. Из города В можем пойти только в городы Д и Г. Из города Г можем пойти только в городы Д и Е. Из города Д можем пойти только в город К. В городах Е, Ж и К путей больше нет.
Чтобы найти M (количество путей от Г до К), мы можем использовать аналогичный подход. Из города Г можем пойти только в городы Д и Е. Из города Д можем пойти только в город К. В городах Е, Ж и К путей больше нет.
Таким образом, для нахождения N и M мы можем рассмотреть следующие маршруты:
N (количество путей от А до Г):
1. А - Б - В - Г
2. А - Б - Г
3. А - В - Г
M (количество путей от Г до К):
1. Г - Д - К
2. Г - Е - К
Теперь мы можем посчитать количество путей от А до К через Г, умножив количество путей от А до Г (N) на количество путей от Г до К (M).
Таким образом, количество различных путей из города А в город К, проходящих через город Г, равно N * M = 3 * 2 = 6.
Итак, существует 6 различных путей из города А в город К, проходящих через город Г.