Здравствуйте решить задания Задан вектор a(2;-4) и точка A (−6; 2). Запишите уравнения прямой, проходящей через точку A, если:

б) вектор a является вектором нормали
б) вектор а является вектором нормали

Задан вектор a(2;-4) и точка A (−6; 2). Запишите уравнения прямой, проходящей через точку A, если:

б) вектор a является вектором нормали.

Если известна некоторая точка M(xo; yo), принадлежащая прямой, и вектор нормали n(n1; n2) этой прямой, то уравнение данной прямой выражается формулой:  

n1*(x – xo) + n2(y – yo) = 0.

Подставим данные в формулу.

2(x+ 6) - 4(y - 2) = 0, раскроем скобки.

2x + 12 - 4y + 8 = 0 и получаем общий вид уравнения:

2x - 4y + 20 = 0 можно сократить на 2:

x - 2y + 10 = 0.

б)  если  вектор нормали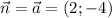    , то уравнение прямой имеет

вид:        .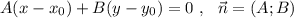

a)  если вектор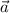  - это направляющий вектор  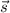 , то каноническое уравнение прямой имеет вид: