Задачи на готовых чертежах. 2

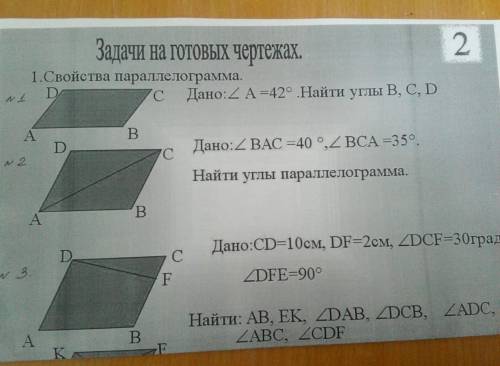
1. Свойства параллелограмма.

C Дано: =42° . Найти углы В, С, D

B

Дано: BAC =40 °, BCA =35°

2

Найти углы параллелограмма.

B

Дано:CD=10cm, DF=2cm, ZDCF=30град

3.

2DFE=90°

Найти: AB, EK, ZDUB, ZDCB, ZADC,

Zabc, 2cdf
​

1. Для решения первой задачи по свойствам параллелограмма, нам дано, что угол C равен 42°.
Найдем углы B, D и C.

В параллелограмме смежные углы суммируются до 180°. Также, противоположные углы параллелограмма равны.

Учитывая, что полная сумма углов в параллелограмме равна 360°, мы можем записать следующие уравнения:
B + C = 180° (1)
C + D = 180° (2)
A + B + C + D = 360° (3)

Заменим значение C в уравнениях (1) и (3), и получим:
B + 42° = 180° --> B = 180° - 42° --> B = 138° (4)

C + D = 180° --> 42° + D = 180° --> D = 180° - 42° --> D = 138° (5)

Заменим значения B и D в уравнении (3), и получим:
A + 138° + 42° + 138° = 360° --> A + 318° = 360° --> A = 360° - 318° --> A = 42° (6)

Таким образом, углы B, C и D равны 138°, а угол A равен 42°.

2. Во второй задаче нам дано: CD = 10см, DF = 2см, и угол DCF = 30°.
Нам нужно найти углы параллелограмма.

Из свойств параллелограмма, противоположные стороны и углы равны.
Значит, угол FCD = 30°, и угол EDF = 30°.

Также, мы можем использовать свойство параллелограмма, что смежные углы дополняются до 180°.
Значит, угол DFE = 180° - 30° - 30° = 120°.

Используя свойства треугольника, мы можем найти угол EFD.
Сумма углов треугольника равна 180°, поэтому:
EFD = 180° - 120° - 30° = 30°.

Таким образом, углы параллелограмма равны:
FCD = 30°, EFD = 30°, DFE = 120° и EDF = 30°.

3. В третьей задаче нам дано, что угол DFE = 90° и нам нужно найти значения AB, EK, ZDUB, ZDCB, ZADC, Zabc, 2cdf.

Зная, что противоположные стороны и углы в параллелограмме равны, мы можем выводить информацию о сторонах и углах в параллелограмме.

Поскольку DFE = 90°, это означает, что D и E находятся на одном диагональном отрезке параллелограмма.
Также, мы можем заметить, что сторона DE равна стороне DF и сторона ED равна стороне DE.

Значит, DE = DF = 2см.

Зная длины сторон и один из углов, мы можем использовать законы косинусов или теорему Пифагора, чтобы найти остальные стороны и углы параллелограмма.

Но, без дополнительной информации или углов, необходимой для расчета, ответ невозможно найти.