Задача для гениев. Есть две рейки (каждая из который длиной в 3 см), первая из них может свободно вращаться на 360 градусов, и к ней прикреплена вторая рейка, которая может вращаться тоже на 360 градусов относительно второй.Есть ли формула, чтобы вычислить угол обеих, чтобы край второй рейки, допустим, достиг точки (4, 5)

Другие вопросы по теме Геометрия
Популярные вопросы
- Война начинается всегда внезапно, хотя для историков она покажется не избежной....
3 - Подчеркните глаголы в неопределённой форме. На деревянном столе лежит черно-белая...
1 - Описать механизм поведения проводников и диэлектриков....
2 - нужно. Rewrite the sentences using Reported Speech 1) We will reach out destination...
2 - Как размножается камнеломка...
2 - ТЕКСТ МОЖЕТЕ НЕ ПИСАТЬ, ТОЛЬКО 2 И 3 ЗАДАНИЕ. Благадарю, кто Засуха возникает (в)следстви.....
2 - У арбуза круглая форма доминирует над удлиненной, зеленая корка - над пятнистой...
2 - решить уравнение (х 2-10) 2+2(х 2-10)+1=0...
1 - Каким должен быть вес шара, чтобы держать балку в равновесии? Вес шара:...Н...
1 - по людски последний, а надо, я вас умоляю, с Дано и си...
2
Объяснение:
При длине рейки в 3 см достичь точки (4,5) невозможно, поскольку расстояние от начала первой рейки до конца второй (в случае, если обе рейки лежат на одной прямой) составляет 3 + 3 = 6 см, а кратчайшее расстояние до точки (4,5) составляет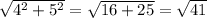 , что больше 6.
, что больше 6.
Допустим, нужная нам точка имеет координаты (x,y), а длина рейки равна S. Тогда кратчайшее расстояние до точки равно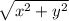 , и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и
, и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и 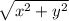 .
.
По теореме косинусов в треугольнике со сторонами a, b и c и углом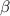 справедливо соотношение
справедливо соотношение 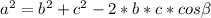 . Для нашего треугольника данное выражение примет вид
. Для нашего треугольника данное выражение примет вид 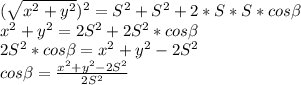
Отсюда искомый угол будет равен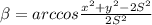 .
.