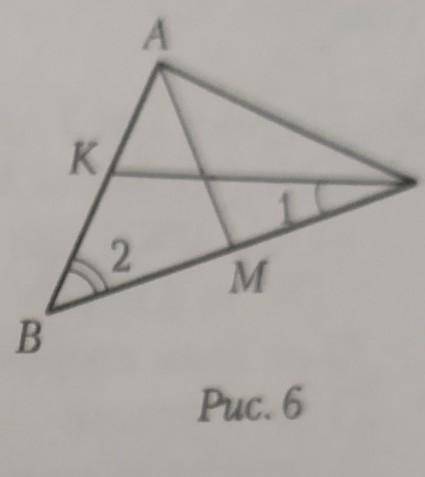
в треугольнике АВС (рис.6) СК и АМ -биссектрисы, ВМ:ВС = 1:2, угол 1=24°, угол 2=х°. Найдите число х​

Для решения данной задачи, нам понадобятся два ключевых факта о биссектрисах треугольника:

1. Биссектриса треугольника делит противолежащий ей угол на две равные части. То есть, в данном случае, угол 1 равен углу 2.

2. Биссектриса также делит противолежащую ей сторону в соотношении длин остальных двух сторон треугольника. В данной задаче, ВМ делит ВС в соотношении 1:2. Это означает, что отношение длины ВМ к длине ВС равно 1:2.

Теперь перейдем к решению задачи:

Учитывая первый факт о биссектрисах, угол 1 равен углу 2, то есть, х = 24°.

Теперь учтем второй факт о биссектрисах. ВМ делит ВС в соотношении 1:2. Это означает, что отношение длины ВМ к длине ВС равно 1:2.

Пусть длина ВМ равна х. Тогда длина ВС будет равна 2х, так как ВМ делит ВС в соотношении 1:2.

Теперь у нас есть два равнобедренных треугольника, АМС и ВМС, где АМ и ВМ являются биссектрисами.

Используем сумму углов треугольника. У треугольника АМС c углом 1=24°, сумма углов будет равна 180°:

24° + 2х + угол 3 = 180°,

где угол 3 - это угол между биссектрисами АМ и СК треугольника АВС.

Так как сумма углов треугольника равна 180°, то:

2х + угол 3 = 180° - 24° = 156°.

Учитывая, что угол 1 равен углу 2, то угол 3 можно найти, вычитая 24° из 156°:

угол 3 = 156° - 24° = 132°.

Таким образом, получаем, что х = 24° и угол 3 = 132°.