Высота равнобедренного треугольника, проведенная к его основанию, равна 4. длина основания равна 6. найдите длину высоты, проведенной к боковой стороне треугольника.
Другие вопросы по теме Геометрия
Популярные вопросы
- Казак тили 6 сынып 60 бет 3 тапсырма...
2 - Почему не стареет комедия Грибоедова Горе от ума ?...
2 - Write affirmative or negative sumattive...
2 - Здравствуйте дети! Меня зовут Ержан Александрович. На улице Абая открылась...
1 - Как вы понимаете смысл следующих пословиц вода сильная вода мельницу...
2 - Среди действительных чисел π, √49 , 1/2 , 1/√49 , 1,8 выберите иррациональное...
3 - В данных записях найдите коды ASCII трех знакова) 1010010010110101101111101...
1 - Б Закончить уравнения реакций, протекание которых возможно (!); уравнять;...
2 - У...ого костра, с...его поля, вокруг ...ого дома, от ...его солнца...
2 - Функции заданы формулами f(x)=14x2 и g(x)=13x2. Вычисли f(−8)g(9)(ответ...
2
Пусть АВС-равнобедренный треугольник с основанием АС=6 и высотой ВН=4.
Т.к. высота, проведенная к основанию равнобедренного треугольника, является медианой, то она делит треугольник на два равных прямоугольных треугольника АНВ и СНВ. При этом АН=СН=3.
В треугольнике СНВ по теореме Пифагора
ВС=5
Найдем площадь треугольника АВС: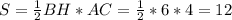
Длину высоты АМ , проведенной к боковой стороне, найдем по такой же формуле: