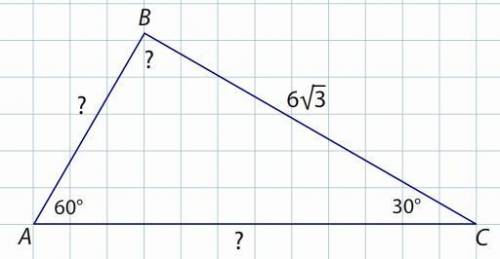
Вычислите неизвестные элементы треугольника и найдите отношения стороны треугольника к синусу противолежащего угла

Давайте рассмотрим данный треугольник и найдем неизвестные элементы. В треугольнике даны следующие известные элементы: AB = 5cm - сторона треугольника AВ BC = 7cm - сторона треугольника ВC AC - гипотенуза треугольника АС sin A = 0.6 - синус угла А Чтобы найти неизвестные элементы, мы можем воспользоваться теоремой Пифагора и определением синуса в прямоугольном треугольнике. 1. По теореме Пифагора мы знаем, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Применим теорему Пифагора для треугольника АСВ: AB^2 + BC^2 = AC^2 5^2 + 7^2 = AC^2 25 + 49 = AC^2 74 = AC^2 Таким образом, AC = √74 2. Теперь давайте найдем значение угла А. По определению синуса противолежащего угла, sin A = противолежащая сторона / гипотенуза. Мы знаем, что sin A = 0.6 и AC = √74. Подставим эти значения в формулу: 0.6 = противолежащая сторона / √74 Умножим обе части уравнения на √74: 0.6 * √74 = противолежащая сторона Получаем: противолежащая сторона = 0.6 * √74 3. Осталось найти отношение стороны треугольника к синусу противолежащего угла. Мы знаем, что это отношение равно: сторона / sin A Подставим значения стороны и sin A: сторона = 5cm sin A = 0.6 Отношение стороны к синусу A = 5cm / 0.6 = 8.33 Таким образом, ответом на вопрос является: сторона треугольника относится к синусу противолежащего угла как 8.33.