Вычислите длину окружности заданной уравнением 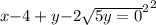
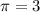
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите дробно-рациональное уравнение...
1 - Знайдіть роботу, яку здійснює автомобіль масою 500 кг на кожних 100 м шляху,...
1 - Тема: успех интервью зависит только от интервьюера. Составьте диалог на эту тему....
1 - Что такое бастер?слово что означает ?...
3 - Знайти градусний кут,якщо градусна міра дуги, на яку він спирається, дорівнює...
2 - Порівняйте хламідомонаду і улотрикс: середовище існування; кількість клітин;...
3 - Пушкин Пророк пересказать на современном русском языке...
1 - исследовать функцию и используя результаты исследования построить график...
1 - Рассказ „ Мальчики ” Достоевский Именно задание: Какой эпизод меня взволновал...
3 - Віднімаємо на основі правила віднімання числа від суми...
3
Уравнение окружности имеет вид :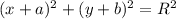 , где (a,b) - координаты центра окружности, а R - это его радиус
, где (a,b) - координаты центра окружности, а R - это его радиус
Постараемся привести наше уравнение к "приличному" ввиду :
Теперь наше уравнение похоже на уравнение окружности, где :
Длинна окружности = 2πR = 2 * 3 * 3 = 2 * 9 = 18
ответ : 18