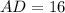Втреугольнике медиана проведенная к стороне образует угол 60 градусов. две другие стороны равны 14 и 2√97. найдите медиану.
Другие вопросы по теме Геометрия
Популярные вопросы
- При каком значении a уравнение (2+а)x=10 1) имеет корень равный...
1 - Синоніми та антоніни до слів «згубився , кликав, чиста,совість...
2 - Надеюсь на вашу comparative & superlative structures пример:...
2 - Запишіть слова фонетичною транскрипцією. визначте асиміляцію...
3 - Напишите на казахском менің өнерім туралы шығарма...
2 - Перемены в культуре россии в годы петровских реформ краткий...
3 - Фрагмент кодирующей цепи днк имеет следующую последовательность...
2 - Complete the questions and answer them. 1. you live in london...
1 - Складіть фонетичні таблиці із цих слів легко джут усміхаеться...
3 - При каком значении переменной выражение не имеет смысла 3х/2х-7...
1
Рассмотрим треугольник ABD. По теореме косинусов
Для треугольника BDC (∠BDC = 180°-60° = 120°), по теореме косинусов:
Поскольку BD - медиана, то AD = CD. Решим систему
Получится и
и 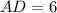 или
или 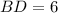 и
и