1. Геометрия
  2. Впрямоугольнике диагональ равна

Впрямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. найдите площадь прямоугольника, делённую на √3

SamaraArtem24 SamaraArtem24    1   13.09.2019 02:50    5

Ответы
LionesBastia LionesBastia  07.10.2020 10:58

25

Объяснение:

Дано:

ABCD - прямоугольник

AC = 10 - диагональ,

∠CAD = 30°

Найти: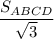 \dfrac{S_{ABCD}}{\sqrt 3}

\displaystyle S_{ABCD} = AD \cdot CD

Рассмотрим ΔACD - прямоугольный, ∠ADC = 90°, AC - гипотенуза

∠CAD = 30° ⇒ CD = 5 (катет, противолежащий углу в 30°, равен половине гипотенузы)

Найдём AD по теореме Пифагора:

\displaystyle AD^2 + CD^2 = AC^2 \\ \\ AD^2 = AC^2 - CD^2 \\ \\ AD^2 = 10^2 - 5^2 = 100 - 25 = 75 \\ \\ AD = \sqrt {75} = \sqrt{25 \cdot 3} = 5 \sqrt 3

Найдём площадь прямоугольника ABCD:

\displaystyle S_{ABCD} = AD \cdot CD = 5\sqrt 3 \cdot 5 = 25\sqrt 3 \\ \\ \frac{S_{ABCD} }{\sqrt 3} = \frac{25 \sqrt 3}{\sqrt 3} = 25


Впрямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. найдите площадь пр
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
timkoa timkoa  08.04.2020 12:58
Правильная четырёхугольная призма вписана в цилиндр. Высота призмы равна 13см , а сторона её основания равна 12см . Вычисли объём цилиндра....
Denis99133 Denis99133  08.04.2020 12:58
В прямоугольном треугольнике АВС гипотенуза АС равна 13 см, катет АВ равен 12 см, катет ВС равен 5 см. Найдите sinC....
КристинаМельникова КристинаМельникова  08.04.2020 12:58
Бісектриса кута прямокутника ділить сторону на відрізки, у відношенні 1:3, починаючи від вершини протилежного кута. Обчисліть площу прямокутника, якщо діагональ...
alamakarova alamakarova  08.04.2020 12:58
Вокруг куба описан цилиндр. Ребро куба равно 6см. Вычисли объём цилиндра....
polycov200412 polycov200412  08.04.2020 12:58
DABC - правильная треугольная пирамида,сторона основания которой ? см,а боковое ребро 5 см. МС - медиана ABC. Найдите площадь MDC (воспользоваться тем,что в основании...
куликов44443456 куликов44443456  08.04.2020 12:57
Підлога кімнати має квадратну форму. її довжина 6м. скільки квадратних плиток зі стороною 3 на 3 дм потрібно, щоб покрыты всю підлогу​...
ВаняАВЕР2006 ВаняАВЕР2006  08.04.2020 12:57
СЧРОЧНО бала) Вибрати вірне твердження. Косинусом гострого кута називається відношення а) протилежного катета до прилеглого; б) прилеглого катета до гіпотенузи;...
Elya100000 Elya100000  20.10.2021 07:56
ОМ биссектриса угла NOL Найдите угол KON, если угол NOM=60°Постройте угол KOР, который будет вертикальный LOMРассчитайте кго грабустную меру Сколько градусов будет...
VASEK191911 VASEK191911  20.10.2021 07:56
у скільки разів збільшиться площа бічної поверхні прямого конуса, якщо радіус основи збільшити в 5 разів ,а висоту в 3 рази...
daniktsarev daniktsarev  20.10.2021 07:58
2. A(7; 3), B(-3; 2) и С(2; 4) нүктелері берілген. АВ = CD тендiгi орындалатындай D(x, y) нүктесінің координатасын табыңдар. 4. 4(5; — 2) және b(2; m) берілсе,...

Популярные вопросы