Внутри квадрата abcd со стороной 1 произвольным образом выбирается точка m. найдите наименьшее возможное значение выражения |ma|+|mb|+|mc|+|md| в качестве ответа укажите квадрат этого числа.
Ответы
Выберем произвольно точку 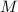 тогда по неравенству треугольников в треугольнике
тогда по неравенству треугольников в треугольнике 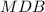 получим
получим 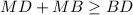 причем последнее равенство выполняется когда
причем последнее равенство выполняется когда 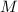 есть точка пересечения диагоналей , аналогично и для треугольника
есть точка пересечения диагоналей , аналогично и для треугольника 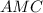 , получим
, получим 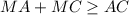 суммируя
суммируя 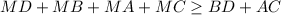 тогда для того чтобы сумма была минимальной , точка
тогда для того чтобы сумма была минимальной , точка 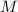 должна являться точкой пересечения диагоналей
должна являться точкой пересечения диагоналей 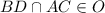 , то есть
, то есть 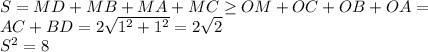
ПОКАЗАТЬ ОТВЕТЫ
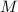 тогда по неравенству треугольников в треугольнике
тогда по неравенству треугольников в треугольнике 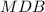 получим
получим 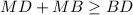 причем последнее равенство выполняется когда
причем последнее равенство выполняется когда 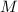 есть точка пересечения диагоналей , аналогично и для треугольника
есть точка пересечения диагоналей , аналогично и для треугольника 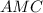 , получим
, получим 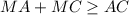 суммируя
суммируя 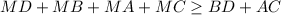 тогда для того чтобы сумма была минимальной , точка
тогда для того чтобы сумма была минимальной , точка 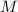 должна являться точкой пересечения диагоналей
должна являться точкой пересечения диагоналей 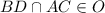 , то есть
, то есть 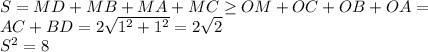
Другие вопросы по теме Геометрия
Популярные вопросы
- B)Al(OH)3 + 3H+ = Al3+ + 3H2Or) Cu2+ + S2- = CustA) Mn + + 2OH = Mn(OH)212+....
2 - Какие ожидания вызывают у вас. Перечисляю частушка, былина, детектив,...
2 - Сравни народную мудрость высказана в пословицах и народное представление...
3 - Матрицы, операции над матрицами...
3 - решить. Нужно начертить в конце какую-то полоску где безконечности....
1 - Города Гочино и Цареградцево соединены прямой дорогой. На дороге стоят...
1 - Коли колеса автомобіля проковзують під час буксування, то сила тяги...
3 - Сторона квадрата дорівнює 6 см. Знайти довжину кола, вписаного в цей...
1 - на бум не писать, а то буду забирать...
1 - Какое слово здесь зашифровано?13 . РОФОВЕТС ...
1