Вершины треугольника АВС находятся в точка А(1,0,2) В(3,3,3) С(2,1,0) найти: а)внешний угол при вершине В б)длины сторон треугольника.
ответ: П-arcos 1/14; Корень из 14,корень из 14 и корень из 6

Вершины ΔАВС находятся в точка А(1,0,2) В(3,3,3) С(2,1,0) найти: а)внешний угол при вершине В  , б)длины сторон треугольника.

Объяснение:

а)Пусть внешний угол при вершине В будет β. Тогда β=180°-∠АВС , по т. о смежных углах.

BA*ВC=|BA|*|BC|cos(∠АВС) .

Координаты векторов ВА(-2;3;-1) , ВC(-1;-2;-3), длины векторов

|BA|=АВ=√( (-2)²+3²+(-1)²)=√14,

|BC|=√( (-1)²+(-2)²+(-3)²)=√14,

2-6+3=√14*√14*cos(∠АВС),   cos(∠АВС)=  ,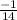  

∠АВС=arccos(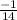 )=π-arccos( )

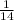Тогда β=180-(π-arccos(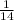 ) )=arccos( )

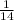б)АВ=√( (3-1)²+(3-0)²+(3-2)²)=√14,

ВС=√( (2-3)²+(1-3)²+(0-3)²)=√14,

АС=√( (2-1)²+(1-0)²+(0-2)² )=√6.