В треугольнике АВС угол С = 90°, угол В=60°, сумма гипотенузы и меньшего катета равна 30 см. Найти СВ.​

10 см.

Объяснение:

✓РЕШЕНО МУДROST✓

Если ∠С = 90°, а ∠В=60°, то

∠А=180°-(90°+60°)=180°-150°=30°-по теореме о сумме углов в треугольнике.

В условии сказано что сумма гипотенузы и меньшего катета равна 30 см. Чтобы понять какой катет меньший, для это нужно посмотреть на углы, которые находятся напротив катетов. Напротив ∠А находится самый маленький катет, т.к ∠А самый маленький в этом треугольнике.

Значит, СВ+АВ=30 см.

Напротив угла равного 30° лежит катет СВ⇒ он равен половине гипотенузы АВ.

Пусть х см - гипотенуза АВ, то

СВ=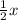

Составим и решим уравнение:

x+0,5х=30

1,5х=30

х=30:1,5

х=20

Итак: гипотенуза АВ=20 см, тогда

СВ=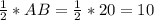 см.

✓РЕШЕНО МУДROST✓