В трапеции ABCD с основаниями АВ и CD диагонали пересекаются в точке Е. Площадь треугольника АВЕ равна 72, площадь треугольника CDE равна 50. Найдите площадь трапеции ABCD.
Другие вопросы по теме Геометрия
Популярные вопросы
- Срешением , нужны . по теме сцепленных полов с признаком 1. гипертрихоз...
1 - Неопределённая форма глаголов: алеет, светлеет, яснеет, разгорается, всплывает,...
1 - Четыре брата юра,петя,вова,и коля-учится в 1, 2, 3,и 4 классах. петя-отличник,...
2 - Полифония в живописи (картинки)ps.это музыка...
1 - Вычислите, какой объём займёт кислород при н.у. массой 8г...
2 - Вшколе обучается 1150 учащихся.девочек на 4% больше,чем мальчиков.сколько...
2 - Нужно решить 163z-157z+627=999 найти значение z 5х+4х=866-261-200 найти...
3 - Угол при вершине равнобедренного тр-ка равен 120 градусов,а боковая сторона...
3 - 2целых 7/3 умножать на 3 целых 5/8= ? желательно с пояснением 2 целых 7/3....
3 - Сложное предложение на тему весна идет с предлогом или...
2
242
Объяснение:
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её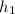 ). Тогда справедливо следующее равенство:
). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме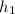 и
и 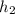 , то есть
, то есть