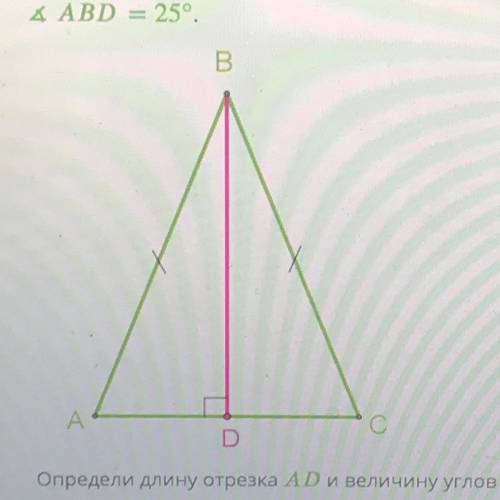
В равнобедренном треугольнике АВС проведена высота к основанию АС, длина основания равна 28см, угол АВD = 25 градусов. Определи длину отрезка АD и величину углов CBD и ABC
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите уравнение в зависимости от значений параметра...
3 - Мнение сочинение Ремарк три товарища...
1 - Определите степень окисления марганца в молекуле КMnO4...
3 - А 1. В каком слове все согласные звонкие? 1) открытка 2) снежный 3)...
2 - перевести текст в косвенную речь A.: Porter, will you see to my luggage,...
3 - Какую работу (кДж) нужно совершить, чтобы вытащить плавающий ледяной...
3 - Задание № 9. Перепишите и переведите предложения на русский язык. Выпишите...
2 - Бежавшая из Крыма армия генерала ... в Европе обрела новое оформление...
3 - 21. Я приехал в Москву 7 сентября ... 22. Мой друг приехал 23 августа....
3 - Определить передаточное число u, если диаметр маховичка D=300мм ход...
3
AC^2 = AD * DC
Поскольку треугольник АВС является равнобедренным, то мы знаем, что угол АBC равен углу АCB и обозначим эту меру угла как х.
Также, поскольку угол АВD равен 25 градусам, угол ADB равен 180 - 25 - 25 = 130 градусам.
Длина основания треугольника АС равна 28 см, поэтому АС = 28 см.
Из уравнения Пифагора в треугольнике АDC мы можем определить длину отрезка DC:
DC^2 = AC^2 - AD^2
Теперь, с учетом того, что угол АCB равен углу АBC, мы можем записать синусы этих углов:
sin(х) = AD / AC
sin(х) = DC / AC
Подставим значения, которые мы знаем:
sin(х) = AD / 28 и sin(х) = DC / 28
Теперь сравним эти два уравнения, получим:
AD / 28 = DC / 28
Таким образом, AD = DC.
Теперь мы можем записать уравнение Пифагора для треугольника ADB:
AD^2 = AB^2 + BD^2
Из угла ADB мы знаем, что BD = AB * sin(130 градусов), поэтому мы можем записать это уравнение следующим образом:
AD^2 = AB^2 + (AB * sin(130))^2
Теперь мы можем найти значение длины отрезка AD:
AD^2 = AB^2 + (AB * sin(130))^2
AD^2 = AB^2 * (1 + sin^2(130))
AD = AB * sqrt(1 + sin^2(130))
Для нахождения величины углов CBD и ABC мы можем использовать треугольник BDC.
У нас уже есть угол BDC, которым является 130 градусов.
Угол ABC можно найти как разность 180 - х.
Угол CBD можно найти как сумму угла BDC (который равен 130 градусам) и угла ABC.
Таким образом, угол ABC = 180 - х, а угол CBD = 130 + (180 - х).
Надеюсь, что эта подробная информация поможет вам понять и решить задачу! Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать.