В прямой треугольной призме в основании лежит прямоугольный треугольник с гипотенузой 6 см и острым углом 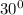. Найдите объем призмы, если длина бокового ребра равна меньшему катету.

ответ: V=13,5√3см³

Объяснение: обозначим вершины призмы А В С Д А1 В1 С1 Д1 с катета и АС, ВС, А1С1, В1С1, угол В=30°. Катет лежащий напротив него равен половине гипотенузы поэтому АС=½×АВ=½×6=3см.

Найдём катет ВС по теореме Пифагора:

ВС²=АВ²-АС²=6²-3²=36-9=27;

ВС=√27=3√3см

Итак: меньший катет- АС, поэтому высоты АА1=ВВ1=СС1=АС=3см

Найдём площадь основания по формуле:

Sосн=½×AC×BC=½×3×3√3=4,5√3см²

Теперь найдём объем призмы по формуле: V=Sосн×АА1=4,5√3×3=13,5√3см³