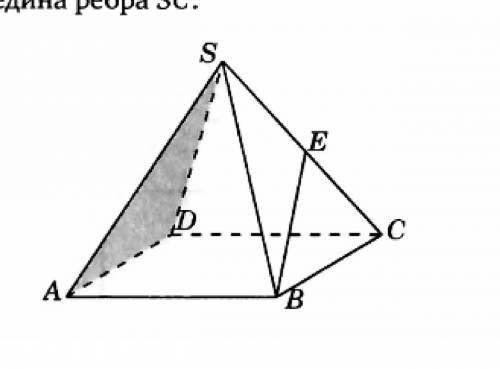
В правильной четырёхугольной пирамиде SABCD, все рёбра которые равны 1, найдите синус угла между прямой BE и плоскостью SAD, где E - середина ребра SC

Для решения данной задачи, нам необходимо вычислить синус угла между прямой BE и плоскостью SAD в правильной четырёхугольной пирамиде SABCD, где E - середина ребра SC.

Для начала нам потребуется найти векторные уравнения прямой BE и плоскости SAD.

1. Векторная прямая BE:
Прямая BE проходит через точки B и E. Мы можем найти направляющий вектор этой прямой, используя координаты этих двух точек.

Так как E - середина ребра SC, то координаты точки E вычисляются как среднее арифметическое координат точек S и C:
E = ( (xS + xC) / 2, (yS + yC) / 2, (zS + zC) / 2 )

Из условия, что все рёбра пирамиды равны 1, мы знаем, что точки S и C имеют координаты (0, 0, 0) и (1, 0, 0) соответственно.

Подставляя эти значения в формулу, получаем:
E = ( (0 + 1) / 2, (0 + 0) / 2, (0 + 0) / 2 )
E = ( 1/2, 0, 0 )

Теперь мы можем найти направляющий вектор прямой BE:
b = EB = E - B = (1/2, 0, 0) - (0, 1, 0) = (1/2, -1, 0)

Таким образом, векторная форма прямой BE имеет вид:
r = B + tb, где r - радиус-вектор точки на прямой BE, B - начальная точка прямой B(0, 1, 0), t - параметр, b - направляющий вектор.

2. Уравнение плоскости SAD:
Плоскость SAD проходит через три точки: S(0, 0, 0), A(0, 1, 0) и D(0, 1, 1). Мы можем составить уравнение плоскости, используя эти три точки.

Уравнение плоскости в координатной форме имеет вид:
Ax + By + Cz + D = 0

Чтобы найти A, B, C и D, мы можем использовать координаты точек S, A и D.

Используя точку S(0, 0, 0) в уравнении, получаем:
0A + 0B + 0C + D = 0
D = 0

Используя точку A(0, 1, 0) в уравнении, получаем:
0A + 1B + 0C + 0 = 0
B = 0

Используя точку D(0, 1, 1) в уравнении, получаем:
0A + 1B + 1C + 0 = 0
C = -B = 0

Таким образом, уравнение плоскости SAD имеет вид:
0x + 0y + 0z + 0 = 0

3. Вычисление синуса угла между прямой BE и плоскостью SAD:
Для вычисления синуса угла между прямой и плоскостью, нам необходимо найти проекцию направляющего вектора прямой на нормальный вектор плоскости.

Нормальный вектор плоскости SAD равен (A, B, C) = (0, 0, 0), так как все коэффициенты равны нулю в уравнении плоскости.

Длина направляющего вектора прямой b равна:
|b| = √( (1/2)^2 + (-1)^2 + 0^2 )
= √( 1/4 + 1 + 0 )
= √( 5/4 )
= √5 / 2

Теперь мы можем найти синус угла между прямой BE и плоскостью SAD по формуле:
sin(θ) = |proj_b (n)| / |b|

Где |proj_b (n)| - длина проекции вектора b на вектор n.

В данном случае, |proj_b (n)| = 0, так как вектор n равен нулю.

Таким образом, синус угла между прямой BE и плоскостью SAD равен 0.

Ответ: Синус угла между прямой BE и плоскостью SAD равен 0.