В пирамиде ABCS ребро AS перпендикулярно основанию ABС и равно 12. Треугольник ABC равносторонний со стороной 4. Найдите высоту AH, проведенную к грани SBC. В ответе укажите значение 13·AH 2.
Другие вопросы по теме Геометрия
Популярные вопросы
- Номер 6822)|783| - х=|-27|=?...
3 - (m-1)(m+1)+1спростіть вираз...
2 - Рассказ И. С. Тургенева Бежин луг. Вопрос 1) почему в рассказе так много описаний....
3 - Заполните таблицу моллюски:система органов,органы, функции...
2 - 2а класс Г.В. Дорофеев Т.Н. Миракова Т.Б. Буква страница84 номер 10...
1 - Найди, какие из суждений верны. А. Для синтеза АТФ и восстановления НАДФ...
2 - Вопросы и задания 1. Раскройте смысл понятия «права и свободы человека и гражданина...
2 - Доберіть українські відповідники до іншомовних слів ефективний, модернізувати,...
2 - Можете , кто знает ответы . I. Inventors (Изобретатели) 1. Only now, after...
1 - Написать о помиловании Марьи Ивановны от 1 лица.Произведение Капитанская дочка...
1
Объяснение:
Дано: Пирамида ABCS, AS ⊥ ABC, AB = AC = BC = 4, AS = 12, AH ⊥ SBC
Найти: AH - ?
Решение: Проведем высоту в треугольнике ΔABC к стороне BC в точку F, так как по условию треугольник ΔABC - равносторонний, то по свойствам равностороннего треугольника его высота является биссектрисой и медианой, следовательно BF = CF. Треугольник ΔCAS = ΔBAS(AS ⊥ ABC по условию, поэтому треугольник ΔCAS и ΔBAS - прямоугольные) по двум катетам, так как AS - общая и AC = BC по условию, из равенства треугольников следует, что SC = SB, тогда треугольник ΔSCB - равнобедренный. Проведем отрезок SF, так как треугольник ΔSCB - равнобедренный(SC = SB, следовательно BC - основание), то по теореме медиана опущенная на высоту является биссектрисой и высотой, тогда SF ⊥ BC.
Так как по условию AH ⊥ SBC, то AH перпендикулярно любой прямой лежащей в плоскости SBC, то AH ⊥ SF (SF ∈ SBC), так как SF - гипотенуза прямоугольного треугольника ΔSAF (по условию AS ⊥ ABC) и так как SF - гипотенуза прямоугольного треугольника ΔSAF (по условию AS ⊥ ABC), то отрезок AH - высота прямоугольного треугольника ΔSAF проведенная к гипотенузе.
Рассмотрим прямоугольный треугольник ΔCAF(AF ⊥ BC по построению). Так как треугольник ΔABC - правильный по условию, то по свойствам правильного треугольника все его углы 60°, следовательно ∠BCA = 60°.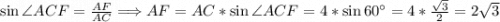 .
.
Рассмотрим треугольник ΔSAF, по теореме Пифагора: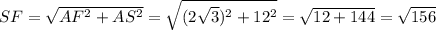 .
.
По формуле площади прямоугольного треугольника: , с другой стороны
, с другой стороны 
AS * AF * 0,5 = AH * SF * 0,5|:0,5SF