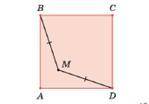
В квадрате ABCD взяли точку M так, что BM = DM. Докажите, что точка M лежит на диагонали квадрата.

Добрый день! Давайте рассмотрим данную задачу.

У нас есть квадрат ABCD, в котором взята точка M так, что BM = DM. Нам нужно доказать, что точка M лежит на диагонали квадрата.

Для начала, давайте обратим внимание на то, что диагонали квадрата равны. Это свойство квадрата.

Так как BM = DM, значит отрезки BM и DM имеют равную длину, они равны между собой.

Пусть AM - это диагональ квадрата, на которой находится точка M. Давайте рассмотрим треугольник ABM.

Очевидно, что у нас есть две равных стороны треугольника: AB, который является стороной квадрата, и BM, который равен DM.

Также, у нас есть угол ABM, который является прямым углом, так как он находится на стороне квадрата.

Из этих данных мы можем заключить, что треугольник ABM является прямоугольным.

Теперь мы можем воспользоваться теоремой Пифагора для прямоугольного треугольника. Эта теорема гласит, что квадрат гипотенузы (стороны напротив прямого угла) равен сумме квадратов катетов (других двух сторон).

В нашем случае, AB является гипотенузой, а BM является одним из катетов.

Таким образом, мы можем записать:

AB^2 = BM^2 + AM^2

Теперь давайте рассмотрим треугольник ADM.

Снова, у нас есть две равные стороны: AD, которая является стороной квадрата, и DM, которая равна BM.

Угол ADM также является прямым углом, так как он находится на стороне квадрата.

Треугольник ADM также является прямоугольным.

Используя теорему Пифагора для треугольника ADM, мы можем записать:

AD^2 = DM^2 + AM^2

Но DM^2 равно BM^2, так как BM = DM.

Таким образом, мы можем записать:

AD^2 = BM^2 + AM^2

Но у нас уже есть такое равенство из рассмотрения треугольника ABM.

Следовательно, AB^2 = AD^2.

Так как квадраты равны между собой, значит и стороны AB и AD тоже равны.

Это свойство прямоугольника - противоположные стороны равны.

Таким образом, точка M лежит на диагонали квадрата.

Однако, мы можем провести еще одно доказательство, используя свойство равных углов, которое гласит, что два угла равны, если у них есть две равные стороны.

Если мы рассмотрим треугольник ABM и треугольник DMС, то у них есть две равные стороны: BM = DM и AB = CD (по свойству квадрата).

Таким образом, угол ABM равен углу DMC.

У нас также есть точка M, которая лежит на стороне DC и находится на диагонали квадрата.

Таким образом, мы доказали, что точка M лежит на диагонали квадрата.

Надеюсь, это доказательство помогло вам понять задачу. Если у вас есть еще вопросы, пожалуйста, задавайте.