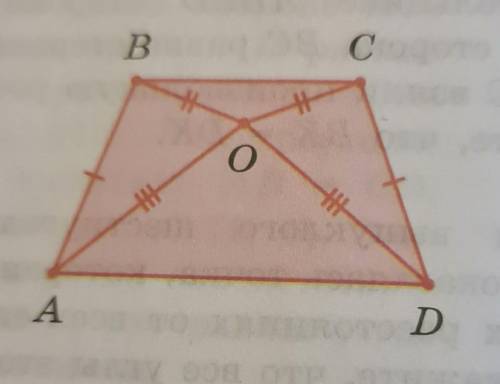
В четырехугольнике ABCD стороны AB и CD равны. Кроме того, внутри него существует такая точка O, что AO = OD, BO = CO.
Докажите, что диагонали этого четырехугольника равны.
Другие вопросы по теме Геометрия
Популярные вопросы
- Морфологический разбор глагола увидел, подошел, появилась...
3 - Что выйлит за 1 четверть ели оценки 2 2 5 5 две двойки за диктант...
3 - 2.что представляет собой духовная сфера? 3.как связаны культура общества и культура...
2 - На стоянке есть 48 автомобилей, из которых 1/6 из них - автобусы, а 3/4 из них...
1 - Найдите ширину окружности, если длина ее радиуса, 2,5 дм...
3 - Неопределённые местоимения к слову человек ?...
2 - Азамат сказал однажды друзьям: позавчера мне было 9 лет, а будущем году мне исполнится...
3 - Объясните написание не- в словах неуклюже, несмотря на, неподвижен, небольшой...
3 - Крестьянин торжествует,на дровах обновляя путь. сделать синтаксический разбор,подписать...
3 - Вычислите количество вещества карбоната калия k2co3 соответствующее 13,8 г...
1
Рассмотрим ∆BOA и ∆COD.
BO=CO по условию;
AB=CD по условию;
АО=DO по условию;
Следовательно ∆ВОА=∆COD по трём сторонам.
Исходя из равенства: угол АВО=угол DCO как соответственные углы равных треугольников. Пусть каждый из этих углов равен х.
Так как ВО=СO, то ∆ВОС – равнобедренный с основанием ВС.
Углы при основании равнобедренного треугольника равны, то есть угол СВО=угол ВСО.
Пусть каждый из них равен z.
Угол АВС=угол АВО+угол СВО=х+z;
Угол DCB=угол DCO+угол ВСО=х+z;
Получим что угол АВС=угол DCB.
Рассмотрим ∆АВС и ∆DCB.
ВС – общая сторона;
Угол АВС=угол DCB (доказано ранее)
АВ=CD по условию;
Следовательно ∆АВС=∆DCB по двум сторонам и углу между ними.
Значит АС=BD как соответственные стороны равных треугольников.
Доказано.