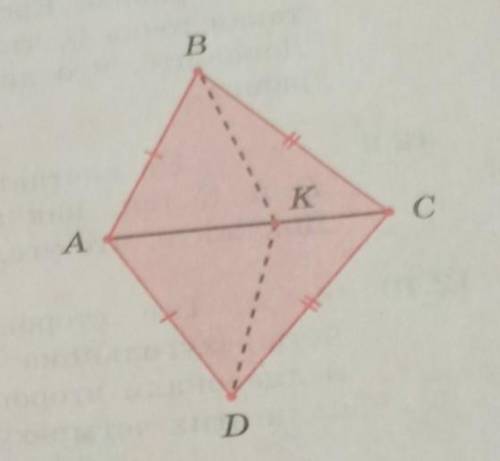
В четырехугольнике ABCD сторона AB равна стороне AD, а сторона ВС равна стороне CD. На его диагонали АС взяли произвольную точку К (рис. 12.14). Докажите, что ВК

Для решения данной задачи, докажем, что треугольник ВКА равнобедренный. Для этого приведем несколько шагов:

Шаг 1: Заметим, что сторона AB равна стороне AD и сторона ВС равна стороне CD. Это означает, что у нас есть две пары равных сторон.

Шаг 2: Посмотрим на треугольники ВАD и ВАB. У них две стороны равны (AB = AD), а третья общая сторона АD. Поэтому треугольники ВАD и ВАB равны по двум сторонам и общей стороне (по правилу ССС равенства треугольников).

Шаг 3: Из равенства треугольников ВАD и ВАB следует, что угол AKD равен углу AKB (по свойству равенства треугольников углы, лежащие напротив равных сторон, равны).

Шаг 4: Так как АК - общая сторона треугольников ВАD и ВАB, а угол AKD равен углу AKB, то треугольники АКД и АКВ равны по двум сторонам и углу. Это означает, что угол КАВ равен углу КДА (по свойству равенства треугольников углы, лежащие напротив равных сторон, равны).

Шаг 5: Поскольку у треугольников АКВ и АКД равны два угла и общая сторона АК, то эти треугольники равны по двум углам и общей стороне (по правилу СУС равенства треугольников).

Шаг 6: Теперь мы знаем, что треугольник ВКА равнобедренный, так как у него две равные стороны (у нас есть доказательство из шага 5).

Шаг 7: Равнобедренный треугольник имеет два равных угла, поэтому у треугольника ВКА угол КВА равен углу КАВ (по свойству равнобедренного треугольника), что означает, что угол КВА равен углу КДA.

Шаг 8: Но угол КВА и угол КДA это один и тот же угол, поскольку это две различные названия для одного угла (угол КВА и угол КДA имеют одну и ту же меру).

Итак, мы получили, что угол КВА равен углу КДA. Это означает, что треугольник КВА равнобедренный, так как у него два равных угла (угол КВА равен углу КДA).

Таким образом, мы доказали, что треугольник ВКА является равнобедренным. В равнобедренном треугольнике равны основания боковых сторон, поэтому ВК = ВА.

Ответ: ВК = ВА.