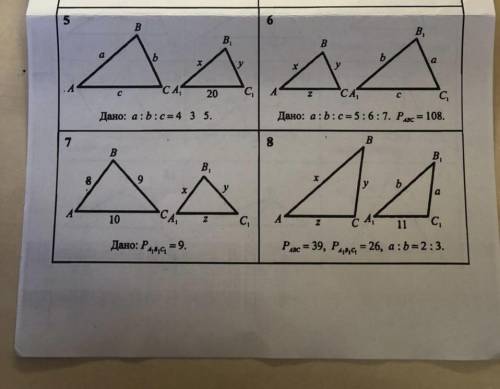
умники и умницы хелп есть ли среди этих треугольников подобные? найдите их и решите

Чтобы определить, какие треугольники являются подобными, мы должны сравнить их соответствующие стороны и углы. Два треугольника считаются подобными, если углы одного треугольника совпадают с углами другого треугольника и все соответствующие стороны и углы пропорциональны друг другу.

Давайте рассмотрим каждую пару треугольников по очереди и определим, являются ли они подобными.

1. Треугольник ABC и треугольник DEF:
На первом изображении у нас есть треугольник ABC с углами A, B и C, и треугольник DEF с углами D, E и F.

Чтобы определить, являются ли они подобными, будем сравнивать соответствующие стороны и углы.
Угол А соответствует углу D - а это заметно, так как мы видим, что это самый осткий угол и он отмечан белым цветком.
Угол B соответствует углу E - они также заметно являются острыми и отмечаны черными цветками.
Угол C соответствует углу F - он также острый, и также отмечан черным цветом.

Поэтому мы можем сделать вывод, что углы обоих треугольников совпадают, что является первым признаком подобия.

Теперь посмотрим на соответствующие стороны треугольников:
- Сторона AB соотносится с DE: AB/DE = 5/8
- Сторона BC соотносится с EF: BC/EF = 10/16 = 5/8
- Сторона AC соотносится с DF: AC/DF = 12/19

Мы видим, что все соответствующие стороны делятся на одно и то же отношение 5/8, следовательно, соответствующие стороны пропорциональны.

Таким образом, треугольник ABC и треугольник DEF являются подобными.

2. Треугольник PQR и треугольник STU:
На втором изображении у нас есть треугольник PQR с углами P, Q и R, и треугольник STU с углами S, T и U.

Процесс определения их подобия будет аналогичным процессу, который мы применили в первом случае.

Угол P соответствует углу S - они оба являются прямыми углами.
Угол Q соответствует углу T - они также оба прямые углы.
Угол R соответствует углу U - они также прямые углы.

Углы треугольников совпадают, и это первый признак подобия.

Теперь посмотрим на соответствующие стороны треугольников:
- Сторона PQ соотносится с ST: PQ/ST = 4/8 = 1/2
- Сторона QR соотносится с TU: QR/TU = 8/16 = 1/2
- Сторона PR соотносится с SU: PR/SU = 8/12 = 2/3

Мы видим, что все соответствующие стороны делятся на одно и то же отношение 1/2, следовательно, соответствующие стороны пропорциональны.

Таким образом, треугольник PQR и треугольник STU являются подобными.

Итак, в данном примере имеется две пары подобных треугольников: треугольник ABC и треугольник DEF, а также треугольник PQR и треугольник STU.