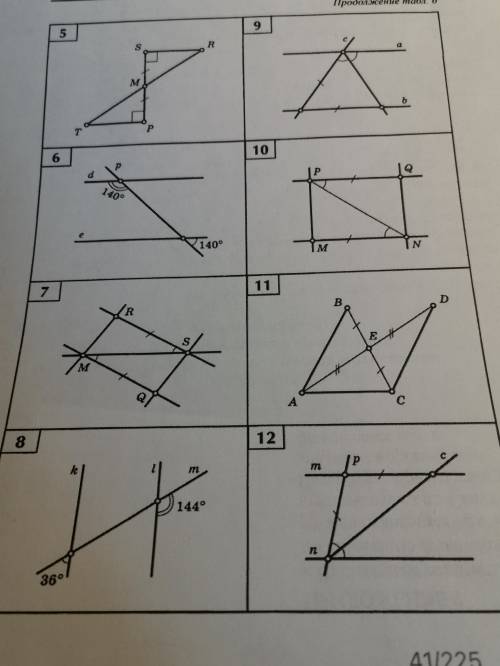
Укажите пары параллельных прямых и докажите их параллельность

На данном изображении мы видим много прямых линий. Чтобы определить пары параллельных прямых, нам нужно вспомнить определение параллельных прямых.

Параллельные прямые - это прямые, которые не пересекаются в любой точке плоскости.
То есть, если мы проведем любую прямую, она будет пересекать только одну из параллельных прямых, но не обе одновременно.

На изображении есть несколько пар прямых, которые могут быть параллельными. Рассмотрим их.

1. Прямая "a" и прямая "d" (помечены цветом синего и красного соответственно).

Чтобы доказать, что эти прямые параллельны, мы можем сравнить углы, образованные этими прямыми и поперечной прямой "t".

Внутренние соответственные углы. Если мы прямоугольник вписываем в "a" и "d". Мы можем увидеть, что углы "с" и "x" являются внутренними соответственные углами. Так как прямая "t" пересекает параллельные прямые "a" и "d", углы с и x должны быть равными.
То есть, угол "с" = угол "x".

Получается, что если мы нарисуем прямую пересечения a и d и проведем перпендикуляр из любой точки, то это будет прямая т (с изображения) и эти прямые никогда не пересекутся. Это значит, что прямые a и d параллельны.

2. Прямая "e" и прямая "f" (помечены цветом зеленого и оранжевого соответственно).

Аналогично предыдущему случаю, чтобы доказать параллельность прямых "e" и "f", мы можем сравнить внутренние соответственные углы.

Мы можем увидеть, что углы "b" и "y" являются внутренними соответственные углами. Так как прямая "t" пересекает эти прямые, углы "b" и "y" должны быть равными.
То есть, угол "b" = угол "y".

Таким образом, прямые "e" и "f" также являются параллельными.

Параллельные прямые:
- а и d
- е и f

При решении задачи мы использовали определение параллельных прямых и свойство внутренних соответственных углов. Это простой и понятный способ доказательства параллельности прямых.