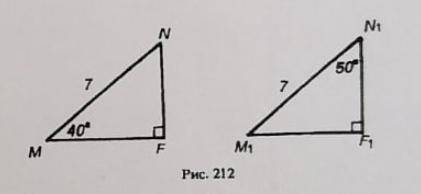
Треугольнике на рисунке 212 прямоугольные. По данным рисунка найдите разность NF=N1F1
Другие вопросы по теме Геометрия
Популярные вопросы
- Где применяется водородный двигатель !!...
3 - Вычисли: 4,05−0,6⋅1,7. ответьте...
2 - 4. Чем интересны другие герои- Капитон (как он сам говорит о себе?),...
3 - Нужно написать переказ тексту який на фото...
2 - Read the information and complete the sentences. Use from...to/until...
3 - Тарас Бульба-характеристика Остапа и его брата по всему произведению...
1 - напишите план Как было написано первое письмо. По Редьярду Киплингу...
2 - Розкрийте проблему синонімії прийменникових конструкцій....
1 - Решите задачи по геометрии с рисунками 1) Периметр квадрата, описанного...
3 - Исследуйте на экстремум функцию z = z(x, y) z = 4x^2 − 3xy + 2y^2...
3
Чтобы решить эту задачу, нужно вспомнить некоторые основные свойства прямоугольных треугольников. Прямоугольный треугольник - это треугольник, у которого один из углов равен 90 градусам. В этой задаче на рисунке дан треугольник АВС, где угол ВАС равен 90 градусам, а стороны АВ и АС называются катетами, а сторона ВС - гипотенузой.
Мы хотим найти разность между отрезками NF и N1F1. Правильнее будет обозначить эти отрезки по-другому. Давай обозначим NF как х, а N1F1 как у.
Теперь давай приступим к решению задачи шаг за шагом:
Шаг 1: Дано прямоугольный треугольник АВС на рисунке 212. Угол ВАС равен 90 градусам.
Шаг 2: Обозначим отрезок NF как х и отрезок N1F1 как у.
Шаг 3: По свойствам прямоугольного треугольника, мы можем использовать теорему Пифагора, чтобы найти отношение между длинами сторон треугольника.
Шаг 4: В треугольнике АВС гипотенуза ВС равна сумме квадратов катетов АВ и АС.
Шаг 5: То есть BC^2 = AB^2 + AC^2.
Шаг 6: Зная, что AB = 29 и AC = 21, мы можем рассчитать BC.
BC^2 = 29^2 + 21^2.
BC^2 = 841 + 441.
BC^2 = 1282.
Шаг 7: Чтобы найти длину отрезка BC, возьмем квадратный корень из обоих сторон уравнения.
BC = корень квадратный из 1282.
BC ≈ 35.83.
Шаг 8: Теперь мы можем использовать соотношение между сторонами треугольника, чтобы найти длину отрезка NF.
NF/BC = х/35.83.
NF = (х/35.83) * BC.
Шаг 9: Аналогично, мы можем использовать соотношение между сторонами треугольника, чтобы найти длину отрезка N1F1.
N1F1/BC = у/35.83.
N1F1 = (у/35.83) * BC.
Итак, мы нашли формулы для вычисления длин отрезков NF и N1F1 в зависимости от их отношений к стороне BC треугольника ВС.
Теперь у нас есть решение задачи, которое мы можем использовать для нахождения значений х и у, если нам будут даны какие-либо числовые значения для отрезков NF и N1F1.