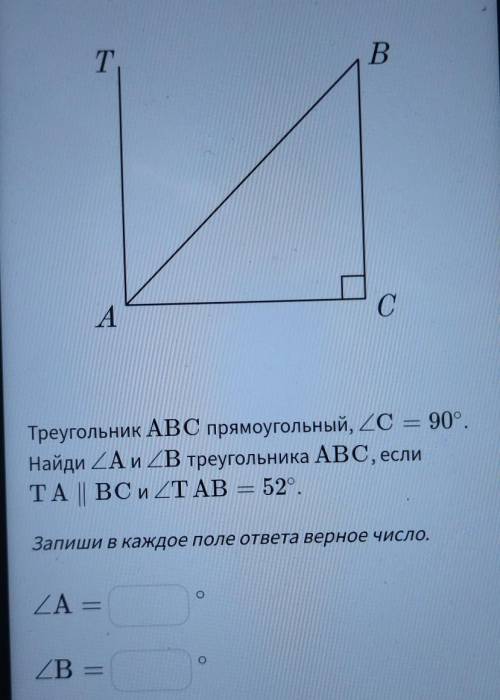
Треугольник ABC прямоугольный, C = 90°. Найди А и В треугольника ABC, если TA||BC и очень )

Для решения данной задачи, нам понадобится использовать соотношение между сторонами и углами в прямоугольном треугольнике.

Из задания дано, что треугольник ABC прямоугольный, то есть угол C равен 90°.
Также дано, что отрезок TA параллелен стороне BC.

Чтобы найти значения углов А и В, нам сначала необходимо определить значение гипотенузы треугольника ABC.

Для этого воспользуемся теоремой Пифагора, которая гласит:
а^2 + b^2 = с^2,
где а и b - катеты, с - гипотенуза.

В данной задачеу нас есть один из катетов - отрезок TA, и гипотенуза треугольника - отрезок TC.
Так как TA параллелен стороне BC, то у нас возникает подобие треугольников и мы можем воспользоваться свойством пропорциональности сторон треугольников.

Итак, обозначим длины сторон треугольника ABC:
- длину стороны AB обозначим как a,
- длину стороны BC обозначим как b,
- длину стороны AC (гипотенузу) обозначим как c.

Тогда по теореме Пифагора у нас есть следующее уравнение:
a^2 + b^2 = c^2.

Также, у нас есть подобие треугольников:
TA/AB = TC/BC.

Заметим, что отрезок TA, по условию, параллелен отрезку BC, поэтому у нас имеется две параллельные прямые. Из теории параллельных прямых следует, что углы А и В являются соответственными углами, и, следовательно, они равны между собой.

Из подобия треугольников TA/AB = TC/BC, получаем следующее уравнение:
TA/AB = TC/BC ⟹ TA/AB = TC/a ⟹ TA*a = AB*TC.

Также, из подобия треугольников TA/AB = TC/BC, следует, что угол В равен 90°, так как угол C равен 90°.

Теперь, используя полученные уравнения и знания о соотношении между сторонами прямоугольного треугольника, можно решить задачу:

1. Найдем значение гипотенузы треугольника ABC, используя теорему Пифагора.
a^2 + b^2 = c^2 ⟹ AB^2 + BC^2 = AC^2 ⟹ 4^2 + 6^2 = AC^2 ⟹ 16 + 36 = AC^2 ⟹ 52 = AC^2.
Извлекаем квадратный корень: AC = √52 = 2√13 (округляем до двух знаков после запятой).
Получаем значение гипотенузы треугольника ABC: AC ≈ 2√13.

2. Решим уравнение, полученное из подобия треугольников:
TA*a = AB*TC.
Из условия задачи, известно, что TA = 12 и TC = 4.
Подставляем известные значения и находим a:
12*a = AB*4.
Так как AB = c (гипотенуза), то AB = 2√13.
Подставляем известное значение AB и находим a:
12*a = 2√13*4 ⟹ 12*a = 8√13.
Делим обе части уравнения на 8:
a = (8√13)/12 ⟹ a = (2√13)/3 (округляем до двух знаков после запятой).
Получаем значение стороны AB: AB ≈ (2√13)/3.

3. Так как угол C равен 90°, и угол В также равен 90°, то углы А и В равны между собой.
Таким образом, получаем ответ: угол А ≈ угол В.

Итак, ответ на задачу:
- Сторона AB треугольника ABC ≈ (2√13)/3.
- Сторона AC (гипотенуза) треугольника ABC ≈ 2√13.
- Угол А ≈ угол В.