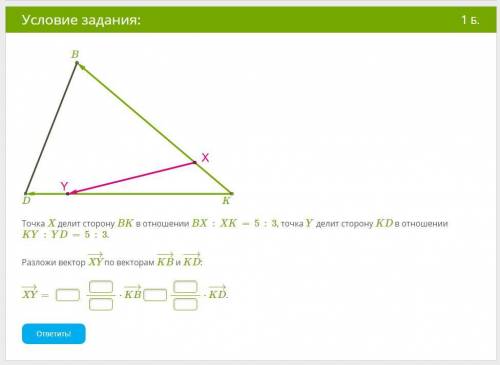
Точка X делит сторону BK в отношении BX:XK=5:3, точка Y делит сторону KD в отношении KY:YD=5:3. Разложи вектор XY−→ по векторам KB−→− и KD−→

Здравствуй!

Для разложения вектора XY -→ по векторам KB -→ и KD -→, вначале нам нужно найти векторы BK -→ и YD -→.

Вектор BK -→ можно найти, зная, что точка X делит сторону BK в отношении BX:XK=5:3. Это значит, что отрезок BK разбивается на 8 равных частей, и точка X находится на 5-й части, а точка K - на 3-й части.

Так как вектор BK -→ направлен от точки B к точке K, то можно сделать вывод, что вектор BK -→ будет равен разности координат K и B:
BK -→ = (xK - xB, yK - yB)

Аналогично, вектор YD -→ можно найти, зная, что точка Y делит сторону KD в отношении KY:YD=5:3. То есть отрезок KD разбивается на 8 равных частей, и точка Y находится на 5-й части, а точка D - на 3-й части.

Итак, вектор YD -→ будет равен:
YD -→ = (xD - xY, yD - yY)

Теперь мы можем разложить вектор XY -→ по векторам KB -→ и KD -→.

Используя свойство разложения векторов, вектор XY -→ может быть представлен в виде суммы разложения вектора по вектору KB -→ и разложения вектора по вектору KD -→.

То есть, XY -→ = XK -→ + KY -→

Используя формулу разложения вектора по вектору, получим:
XK -→ = (xK - xB) * (XB -→ / ||XB -→ ||)
KY -→ = (xD - xY) * (YD -→ / ||YD -→ ||)

Где ||XB -→ || и ||YD -→ || обозначают длины векторов XB -→ и YD -→ соответственно.

Теперь, зная значения точек B, K, Y и D, мы можем вычислить координаты каждого из векторов и получить окончательные ответы.

Надеюсь, это объяснение помогло вам понять, как разложить вектор XY -→ по векторам KB -→ и KD -→. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать! Я всегда готов помочь.