Точки М и N расположены на ребрах треугольной пирамиды Скопируйте рисунок, отметьте и обозначьте точки, в которых прямая MN пересекает прямые, содержащие другие ребра пирамиды. Выберите соответствующую точку.
1. N
2. M
3. T
4. P
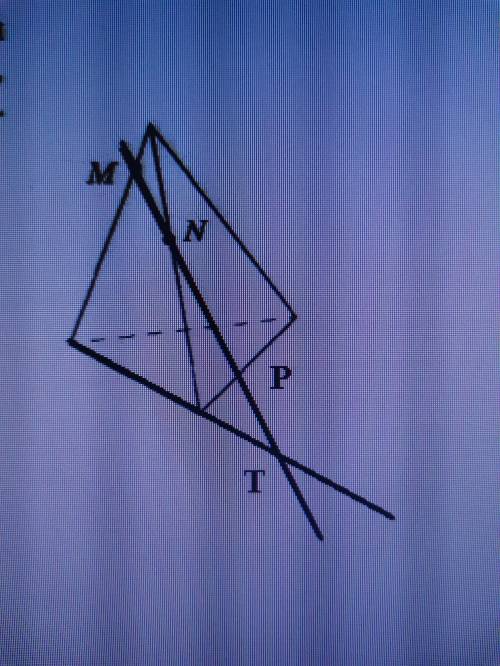
Другие вопросы по теме Геометрия
Популярные вопросы
- Надо сделать сжатое изложение из текста Есть пора в году, когда земля...
3 - кто знает? Отрасль Сельское хозяйство. Нужно ответить на вопросы 1....
2 - ответьте на вопросы скоро ко Что такое увертюра в опере?2 Кто автор...
1 - Match the words to form phrases.Use the phases to complete the sentences....
2 - Хто в Енеїді кружляв сивуху і оселедцем заїдав ?...
1 - Другий паровий двигун у світі? хто створив? рік створення? трошки про...
3 - Почему рафинированные продукты являются нездоровым источником пищи?...
2 - Хромосомы от цитоплазмы отделены...
2 - с немецким - решите задания 1А и 2 (см. прикрепленный файл)...
3 - Заполните пропуски в программе решение задачи сс14 из встроенного задачника...
1
Сначала, чтобы построить прямую MN, мы должны определить координаты точек M и N.
На рисунке, координаты точки M обозначены как (2,4,0), а координаты точки N обозначены как (5,3,1).
Теперь подсчитаем дирекционные векторы для ребер пирамиды.
Для ребра MP, мы имеем дирекционный вектор (3, 2, -1).
Для ребра NP, мы имеем дирекционный вектор (3, -1, 1).
И для ребра TP, мы имеем дирекционный вектор (-2, -1, 1).
Теперь, чтобы определить точку пересечения прямой MN с прямыми, содержащими ребра пирамиды, мы можем использовать параметрические уравнения для каждой прямой.
Для прямой MN, параметрическое уравнение будет выглядеть следующим образом:
x = 2 + 3t
y = 4 + (3 - 1)t
z = 0 + t
Теперь мы можем подставить эти значения в параметрическое уравнение для каждой прямой и решить систему уравнений, чтобы найти точку пересечения.
Для ребра MP, параметрическое уравнение будет выглядеть следующим образом:
x = 2 + 3s
y = 4 + 2s
z = 0 - s
Подставляя значения из параметрического уравнения прямой MN в уравнение для ребра MP, мы получаем следующую систему уравнений:
2 + 3t = 2 + 3s
4 + (3 - 1)t = 4 + 2s
0 + t = 0 - s
Уравнение 1 и уравнение 2 дадут нам:
3t = 3s
3 - t = 2s
Решая это уравнение, мы получаем t = s = 1.
Теперь мы можем подставить это значение в параметрическое уравнение для прямой MN, чтобы найти точку пересечения с ребром MP:
x = 2 + 3(1) = 5
y = 4 + (3 - 1)(1) = 6
z = 0 + 1 = 1
Таким образом, прямая MN пересекает ребро MP в точке P с координатами (5, 6, 1).
Аналогично, мы можем решить для остальных ребер пирамиды, чтобы найти остальные точки пересечения.
Подставляя значения из параметрического уравнения прямой MN в уравнение для ребра NP, мы получаем следующую систему уравнений:
2 + 3t = 3 + 3s
4 + (3 - 1)t = 3 - s
0 + t = 1 + s
Решая это уравнение, мы получаем t = s = 1/2.
Подставляя это значение в параметрическое уравнение для прямой MN, чтобы найти точку пересечения с ребром NP:
x = 2 + 3(1/2) = 3.5
y = 4 + (3 - 1)(1/2) = 4.5
z = 0 + 1/2 = 0.5
Таким образом, прямая MN пересекает ребро NP в точке T с координатами (3.5, 4.5, 0.5).
Подставляя значения из параметрического уравнения прямой MN в уравнение для ребра TP, мы получаем следующую систему уравнений:
2 + 3t = -2 - 2s
4 + (3 - 1)t = -1 - s
0 + t = 1 + s
Решая это уравнение, мы получаем t = -1, s = -1.
Подставляя это значение в параметрическое уравнение для прямой MN, чтобы найти точку пересечения с ребром TP:
x = 2 + 3(-1) = -1
y = 4 + (3 - 1)(-1) = 2
z = 0 + (-1) = -1
Таким образом, прямая MN пересекает ребро TP в точке P с координатами (-1, 2, -1).
Таким образом, прямая MN пересекает ребра MP, NP и TP в точках P, T и N соответственно.
Ответ: 4. P, 3. T, 1. N