Точки A и B лежат в разных полуплоскостях относительно прямойA1B1 .Отрезки AA1 и BB1 перепендикулярны прямой A1B1.Найдите расстояние KK1 от середины K1 отрезка AB до прямой A1B1,если AA1=5 , BB1=11.

KK₁ = 3 ед.

Объяснение:

Дано: прямая АВ;

АК=КВ;

АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ.

АА₁ = 5; ВВ₁ = 11.

Найти: КК₁

Пусть А₁В₁= 2а.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.

Теорема Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

АК = КВ ⇒ А₁К₁ = К₁В₁ = а.

Рассмотрим ΔА₁АО и ΔОВВ₁ - прямоугольные.

Вертикальные угла равны.

∠1 = ∠2 (вертикальные)

⇒ ΔА₁АО ~ ΔОВВ₁  (по двум углам)

Составим пропорцию:

Пусть А₁О = 5х, тогда ОВ₁ = 11х

Составим уравнение:

⇒

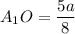
Тогда

Рассмотрим ΔА₁АО и ΔК₁КО - прямоугольные.

∠1=∠2 (вертикальные)

⇒ ΔА₁АО ~ ΔК₁КО

Составим пропорцию: