С ГЕОМЕТРИЙ

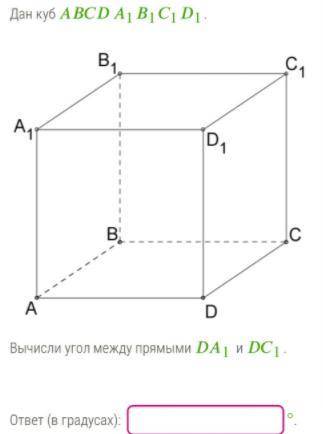
Дан куб ABCDA1B1C1D1

Вычисли угол между прямыми DA1 и DC1

Дай ответ в градусах

Для того чтобы вычислить угол между прямыми DA1 и DC1, нам понадобятся знания о геометрии и основные свойства прямых и плоскостей.

1. Сначала мы должны определить, какие углы имеются в кубе ABCDA1B1C1D1. Поскольку это куб, все грани являются квадратами и углы между сторонами квадратов равны 90 градусам.

2. Обратим внимание на точку A. Из A выходят три ребра: AD, AB и AC. Заметим, что прямые AD и AC лежат в одной плоскости, а прямая AB перпендикулярна к этой плоскости.

3. Рассмотрим треугольник AD1C1. Он образован ребрами AD1, DC1 и AC1 куба. В этом треугольнике есть два угла: угол C1AD1 и угол AAD1, которые нам известны.

4. Определим первый угол: угол C1AD1. Этот угол можно выразить через угол AAD1 и остаток угла между прямыми DA1 и DC1. Допустим, этот остаток угла обозначим как α.

5. Заметим, что два угла, угол AAD1 и угол C1AD1, вместе составляют прямой угол, то есть их сумма равна 180 градусам.

6. Так как угол AAD1 равен 90 градусам, мы можем записать уравнение:
90 + C1AD1 = 180
C1AD1 = 90

7. Теперь мы знаем, что угол C1AD1 равен 90 градусам.

8. Однако нам нужно найти остаток угла между прямыми DA1 и DC1, а не угол C1AD1.

9. Из шага 4 мы знаем, что угол C1AD1 можно выразить через α. Поэтому мы можем записать еще одно уравнение:
C1AD1 = 90 - α

10. Подставим значение угла C1AD1 из шага 6 в уравнение из шага 9:
90 = 90 - α

11. Вычтем 90 с обеих сторон уравнения:
0 = -α

12. Таким образом, получаем, что α равно нулю.

13. Так как α равно нулю, прямые DA1 и DC1 в плоскости треугольника AD1C1 параллельны друг другу.

14. Угол между параллельными прямыми всегда равен 0 градусам.

Ответ: угол между прямыми DA1 и DC1 равен 0 градусам.