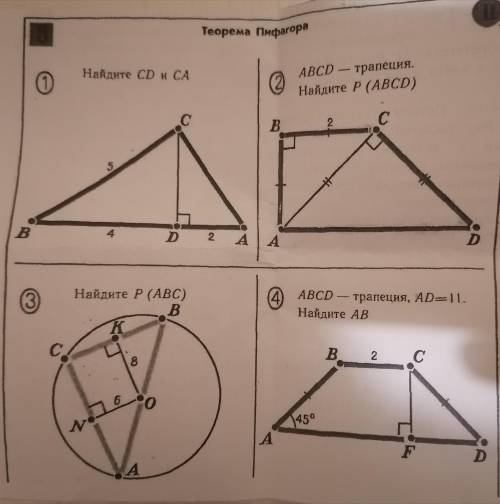
решить задачи по геометрии по теореме Пифагора

Эмм , надеюсь правильно

Объяснение:

Добрый день! Конечно, я могу помочь вам решить задачи по геометрии с использованием теоремы Пифагора.

Дано: у нас есть треугольник ABC со сторонами АВ, ВС и АС (показан он на рисунке). Нужно найти длину стороны ВС, если известны длины сторон АВ и АС.

Шаг 1: Из обозначений на рисунке видно, что развернутый и синий треугольник формируют прямоугольный треугольник АВС, где сторона АС является гипотенузой.

Шаг 2: Мы можем применить теорему Пифагора, которая гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Шаг 3: Применим теорему Пифагора к треугольнику АВС. Пусть длины сторон АВ и АС будут соответственно "a" и "b", а длина стороны ВС - "с". Тогда мы можем записать следующее уравнение:

а^2 + с^2 = b^2

Шаг 4: Подставим известные значения в это уравнение. Из рисунка следует, что длина стороны АВ равна 3, а длина стороны АС равна 4. Подставим эти значения:

3^2 + с^2 = 4^2

9 + с^2 = 16

Шаг 5: Теперь решим уравнение, чтобы найти длину стороны ВС. Вычтем 9 из обеих сторон уравнения:

с^2 = 16 - 9

с^2 = 7

Шаг 6: Чтобы найти значение с, возьмем квадратный корень от обеих сторон уравнения:

c = √7

Шаг 7: Округлим значение √7 до ближайшего целого числа. Получается, что длина стороны ВС равна примерно 2.65 (округляем до двух знаков после запятой).

Таким образом, длина стороны ВС составляет примерно 2.65 единицы длины.