Решения записывать подробно! Задание 4 ( ).

Задана равнобедренная трапеция ABCD. Диагональ AC, равная 6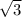, является биссектрисой острого угла A = 60°. Найдите периметр трапеции.

Хорошо, давайте решим эту задачу.

Пусть AB = CD = a - это боковые стороны равнобедренной трапеции ABCD.

Также, пусть BC = d - это основание трапеции.

Мы знаем, что диагональ AC равна 6√3 и является биссектрисой острого угла A = 60°.

Первое, что нам нужно сделать, это найти значение стороны a.

Используя теорему косинусов для треугольника ABC, мы можем записать:

AC^2 = AB^2 + BC^2 - 2 * AB * BC * cos(A)

(6√3)^2 = a^2 + d^2 - 2 * a * d * cos(60°)

Упрощая это уравнение, получаем:

108 = a^2 + d^2 - a * d

Теперь, у нас есть уравнение с двумя неизвестными. Нам нужно найти значение a и d.

Следующий шаг - использовать информацию о том, что трапеция ABCD равнобедренная. В равнобедренной трапеции боковые стороны равны. То есть, a = d.

Подставляем a вместо d в уравнение и получаем:

108 = 2a^2 - a^2

108 = a^2

Теперь мы можем найти значение a, возведя обе части уравнения в квадратный корень:

a = √108

a = 6√3

Теперь, у нас есть значение a, мы можем найти периметр трапеции.

Периметр трапеции (P) равен сумме всех сторон. В нашем случае, P = AB + BC + CD + DA.

P = a + d + a + d

P = 6√3 + 6√3 + 6√3 + 6√3

Упрощаем:

P = 24√3

Таким образом, периметр трапеции равен 24√3.

Надеюсь, эта подробная и обстоятельная информация помогла вам понять, как решить эту задачу! Если у вас возникнут еще вопросы, не стесняйтесь задавать их.