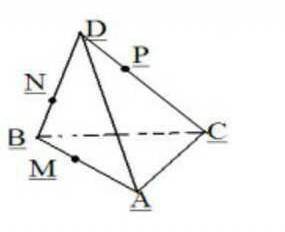
Рассмотрим тетраэдр dabc. построить сечение проходящее через точки m, n, p​

Чтобы построить сечение, проходящее через точки m, n, p тетраэдра dabc, нужно использовать следующий алгоритм.

Шаг 1: Найдите плоскость, проходящую через точки m, n, p.

Для этого можно воспользоваться уравнением плоскости в трехмерном пространстве, например, общим видом главного уравнения плоскости Ax + By + Cz + D = 0.

Построение данной плоскости может быть непростым процессом, поэтому давайте воспользуемся другим способом.

Обратите внимание, что точки m, n, p являются точками пересечения ребер тетраэдра. Это значит, что плоскость, проходящая через эти три точки, также будет содержать отрезки, соединяющие эти точки на тетраэдре dabc.

Шаг 2: Найдите отрезки, соединяющие точки m, n, p на тетраэдре dabc.

Для этого просто проведите линии, проходящие через указанные точки и соединяющие их на тетраэдре. Эти линии будут являться отрезками, которые находятся внутри тетраэдра.

Шаг 3: Постройте плоскость, проходящую через найденные отрезки.

Для этого выберите два отрезка, проведенных в предыдущем шаге. Они должны быть неколлинеарными, то есть не лежать на одной прямой.

Примените закон трех точек для построения плоскости. Вы можете взять точку на одном из отрезков и провести через нее прямую, перпендикулярную этому отрезку. Затем выберите другую точку на втором отрезке и проведите линию, проходящую через эту точку и перпендикулярную первому отрезку. Они пересекутся и образуют третью точку на плоскости.

Повторите эту процедуру для всех возможных пар отрезков. В результате вы получите несколько точек на плоскости.

Шаг 4: Проведите линии, соединяющие полученные точки, чтобы сформировать сечение тетраэдра.

Теперь вы можете провести линии, соединяющие полученные точки на плоскости. Эти линии будут образовывать сечение тетраэдра, проходящее через точки m, n, p.

Обратите внимание, что в зависимости от выбора отрезков в шаге 3 их пересечение на плоскости может быть либо линией, либо точкой.

Это подробное и обстоятельное решение поможет вам лучше понять, как построить сечение тетраэдра, проходящее через точки m, n, p.