Подробное решение Найдите синус и тангенс угла А, если cosА 5/9 и 0< A< 90 градусов

Ответы

dashko4etckowa 19.12.2020 19:10

По основному тригонометрическому тождеству: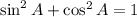 $\sin^2A + \cos^2A = 1$ , откуда:

$\sin A = \sqrt{1-\cos^2A} = \sqrt{1-\left(\dfrac{5}{9}\right)^2} = \sqrt{1 - \dfrac{25}{81}} = \sqrt{\dfrac{56}{81}} = \dfrac{\sqrt{56}}{9} = \boxed{\dfrac{2\sqrt{14}}{9}}$

Тангенс угла равен частному от деления синуса этого угла на косинус.

$tgA = \dfrac{\sin A}{\cos A} = \dfrac{\dfrac{2\sqrt{14}}{9}}{\dfrac{5}{9}} = \boxed{\dfrac{2\sqrt{14}}{5}}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Aleqs2005 14.04.2021 19:25

ВЛЕПЛЮ ВАМ 5 ЗВЁЗДОЧЕК И КОРОНКУ))ТОЛЬКО ПЛЗ ...

жалеоИвантелтуштуш 14.04.2021 19:25

Вычислите площадь трапеции,основания которой равны 9см и 7см, а одна из боковых сторон образует с основанием угол в 30° и равна 8см...

анлггрн765 14.04.2021 19:26

Докажите что : треугольник ABC= треугольнику A1 B1 C1...

unicorn1213 14.04.2021 19:27

1) 2 корень 22 2) 6 корень 2...

идинахер89 18.06.2019 08:50

Одна диагональ ромба 16 см ,а другая на 7 см меньше. найдите площадь....

alinaLodygina 18.06.2019 08:50

Найдите величины углов ромба если одна из его диагоналей образует со стороной угол величиной 20 градусов...

ника2760 07.06.2019 13:10

Втреугольнике abc угол c равен 90°, ab = 70, ac = 56. на продолжении стороны ac за точку a взяли точку d. найдите sin bad...

sasharaiskaja 07.06.2019 13:10

2окружности с центрами в о и к имеют соответственные радиусы 4 и 8 см. найдите радиусы окружностей, касающихся одновременно двух данных если их центры лежат на прямой ок и отрезок...

nastyafifefoks 07.06.2019 13:10

Найдите площадь прямоугольного треугольника,гипотенуза которого равна 26см, а разность катетов-14см...

невідомий34 07.06.2019 13:10

Свойство внешнего угла треугольника...

Подробное решение Найдите синус и тангенс угла А, если cosА 5/9 и 0< A< 90 градусов

Популярные вопросы