По номер 6: рис. 607 дано: угол (ас, bd) =60° найти: ав, аd, sабсd , буду ❣️​

ABCD - прямоугольник, AK - биссектриса, BAK=90/2=45.

В треугольнике с углами 45, 90 стороны относятся как 1:1:√2

AB= AK/√2 =5√2/2

Диагонали прямоугольника равны и точкой пересечения (O) делятся пополам, AO=BO.

△AOB - равнобедренный с углом 60 => равносторонний, ABD=60.

В треугольнике с углами 60, 90 стороны относятся как 1:√3:2

AD= AB*√3 =5√6/2

S(ABCD)= AB*AD =5√2/2 *5√6/2 =25√3/2

Из треугольника ABK:

∠KAD = ∠BKA(как внутренние накрестлежащие)

∠BAK = ∠KAD (по условию)

Значит, ∠BAK = ∠BKA, тогда треугольник ABK - равнобедренный.

Обозначим катеты как X.

Тогда 2x²=25, x=.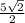

Проведем AD и BC, обозначим точку пересечения O. Тогда ∠COD = 60°,

CO=DO(по свойству прямоугольника), значит треугольник COD - равносторонний.Значит CD=CO=DO=.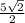

∠BOC = 180-60=120°, тогда из треугольника BOC по теореме косинусов найдем BC.

BC=√25/2+25/2+25/2=.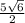

AB=CD=.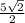

AD=BC=.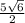

S=AD*BC=5√3.