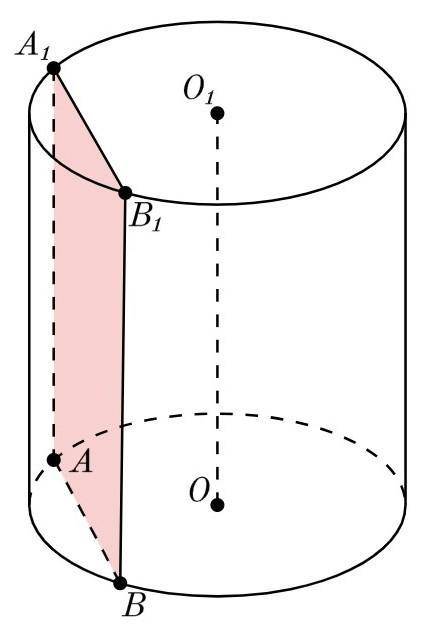
площадь сечения цилиндра плоскостью, параллельной оси цилиндра равна 201. Исходя из данных рисунка, найди косинус угла между плоскостями (A1AB) и (A1AO), если площадь осевого сечения цилиндра равна 536.

Для решения этой задачи нам понадобятся знания о геометрических свойствах цилиндра и понятии угла между плоскостями.

Первым шагом нужно заметить, что сечение цилиндра плоскостью, параллельной его оси (плоскость (A1AB)), является прямоугольником. По условию, площадь этого прямоугольника равна 201.

Длина боковой стороны этого прямоугольника (AB) равна длине окружности основания цилиндра. По формуле длины окружности, длина AB равна 2πR, где R - радиус основания цилиндра.

Поэтому 2πR * h = 201, где h - высота цилиндра.
Таким образом, получается, что 2πR = 201/h.

Далее, нам дано другое сечение цилиндра, осевое сечение. Это сечение является кругом с площадью 536. По формуле площади круга, площадь осевого сечения равна πR^2.

Поэтому πR^2 = 536.

Теперь мы имеем два уравнения:
2πR = 201/h
πR^2 = 536

Можно переписать первое уравнение в виде πR = (201/h)/2. Подставим это во второе уравнение:
(201/h)/2 * R = 536
(201/2h) * R = 536
R^2 = (536 * 2h) / 201
R^2 = (1072h) / 201
R^2 ≈ 5.33h

Теперь приступим к определению косинуса угла между плоскостями (A1AB) и (A1AO).

Вначале заметим, что вектор AO перпендикулярен плоскости (A1AB), так как AO является радиусом цилиндра, а радиус всегда перпендикулярен касательной.

Тогда, давайте рассмотрим проекцию вектора AB на вектор AO. Эта проекция будет представлять собой высоту прямоугольника A1ABO. Обозначим эту проекцию как h1.

Найдем косинус угла между AB и AO. Для этого воспользуемся формулой косинуса угла:
cos(угол) = проекция вектора AB на вектор AO / |AB|

Длина вектора AB равна длине боковой стороны прямоугольника A1AB, то есть 2πR.

Таким образом, cos(угол) = h1 / 2πR.

Мы знаем, что площадь прямоугольника A1AB равна 201. Площадь прямоугольника равна произведению его сторон, поэтому h1 * 2πR = 201.

Теперь мы можем заменить h1 в формуле для косинуса угла:
cos(угол) = h1 / 2πR = 201 / (2πR * 2πR) = 201 / (4π^2 * R^2)

Мы уже выразили R^2 через h. Подставим это в формулу:
cos(угол) = 201 / (4π^2 * 5.33h) = 201 / (21.14π^2 * h)

Таким образом, косинус угла между плоскостями (A1AB) и (A1AO) равен 201 / (21.14π^2 * h).