«Первый и второй признаки равенства треугольников. Равнобедренный треугольник» Задача 1. Периметр равнобедренного треугольника равен 35 см. Найдите стороны этого треугольника, если боковая сторона на 5 см меньше основания.

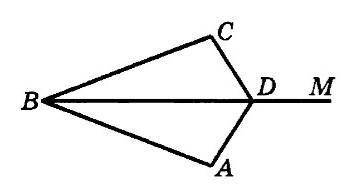
Задача 2. Дано: СО = АО;

∠СВМ = ∠АВМ.

Доказать: ∠А = ∠С.

Задача 3. Периметр равнобедренного треугольника равен 110 см. Какими могут быть стороны треугольника, если две из них относятся как 3:4?​

Задача 1:
Дано, что периметр равнобедренного треугольника равен 35 см и боковая сторона на 5 см меньше основания.

Пусть основание треугольника равно x см. Тогда боковая сторона равна (x - 5) см, так как она на 5 см меньше основания.

Периметр треугольника равен сумме длин всех его сторон. Так как равнобедренный треугольник имеет две равные стороны (боковые стороны), для нахождения периметра треугольника нужно умножить длину одной из боковых сторон на 2, а затем добавить длину основания.

Поэтому, периметр треугольника равен (x - 5) + (x - 5) + x = 3x - 10.

Так как периметр треугольника равен 35 см, мы можем записать уравнение:

3x - 10 = 35

Для решения этого уравнения, добавим 10 к обеим сторонам:

3x = 45

Затем разделим обе стороны на 3:

x = 15

Теперь мы знаем, что основание треугольника равно 15 см.

Для нахождения длины боковой стороны, заменим x в формуле (x - 5):

(15 - 5) = 10

Таким образом, основание треугольника равно 15 см, а боковая сторона равна 10 см.

Ответ: основание треугольника равно 15 см, а боковая сторона равна 10 см.

Задача 2:
Дано, что СО = АО и ∠СВМ = ∠АВМ.

Для доказательства, что ∠А = ∠С, мы можем использовать свойство равнобедренных треугольников, которое говорит, что если две стороны и углы при них одинаковы, то треугольники равнобедренные.

Исходя из условия, у нас есть две равные стороны СО и АО, и два равных угла: ∠СВМ и ∠АВМ.

Следовательно, по первому признаку равенства треугольников, треугольники СВМ и АВМ равнобедренные.

Так как в равнобедренных треугольниках равные углы находятся напротив равных сторон, мы можем сделать вывод, что ∠А = ∠С.

Ответ: ∠А = ∠С.

Задача 3:
Дано, что периметр равнобедренного треугольника равен 110 см, а две из его сторон относятся как 3:4.

Пусть сторона треугольника, относящаяся к меньшей стороне, равна 3x, а сторона, относящаяся к большей стороне, равна 4x, где x - некоторое число.

Так как периметр равен сумме длин всех сторон треугольника, мы можем записать уравнение:

3x + 4x + 4x = 110

Сложим все члены:

11x = 110

Разделим обе стороны на 11:

x = 10

Теперь мы знаем, что x равно 10.

Для нахождения длины сторон треугольника, умножим x на соответствующие коэффициенты:

Меньшая сторона: 3 * 10 = 30
Большая сторона: 4 * 10 = 40

Ответ: меньшая сторона треугольника равна 30 см, а большая сторона равна 40 см.