Окружность касается сторон треугольника, длины которых равны 9, 10 и 11. Найдите длину наибольшего из отрезков, на которые точка касания делит сторону, равную 10.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какие пометы вы употребите,если необходимо объяснить лексическое значение слов...
3 - Из точки а не лежащей в плоскости проведены к этой плоскости перпендикуляр ас...
1 - Цена товара увеличился на 10% в первом, втором и окончательная цена упала на...
3 - Антонимы, характеризующие злого человека...
1 - Сочинение на тему как характер герасима проявился к муму...
2 - Решите уравнение 4x(x-2)-2x(2x-3)=10...
2 - Решить : придумать 5 наречий и проспрегать по сравнительной степени : простая...
2 - Группа из 141 туриста отправилась на экскурсию.50 туристов поехали в большом...
3 - Составить составьте слово из букв e r a m c e c i подсказка: это десерт...
1 - Диагональ ас делит трапецию abcd на два подобных треугольника авс и dca. основания...
3
AC = 10; BC = 11; AB = 9.
Пусть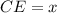 , тогда
, тогда  (как касательные к окружности). Тогда
(как касательные к окружности). Тогда 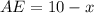 и
и 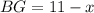 . Тогда
. Тогда 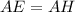 и
и 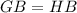 (как касательные к окружности).
(как касательные к окружности).
Тогда AE = 10 - 6 = 4, откуда наибольший отрезок будет CE = 6
ответ: 6.