Объясните как это делать, ну и решать. Прямо объяснение нужно четкое
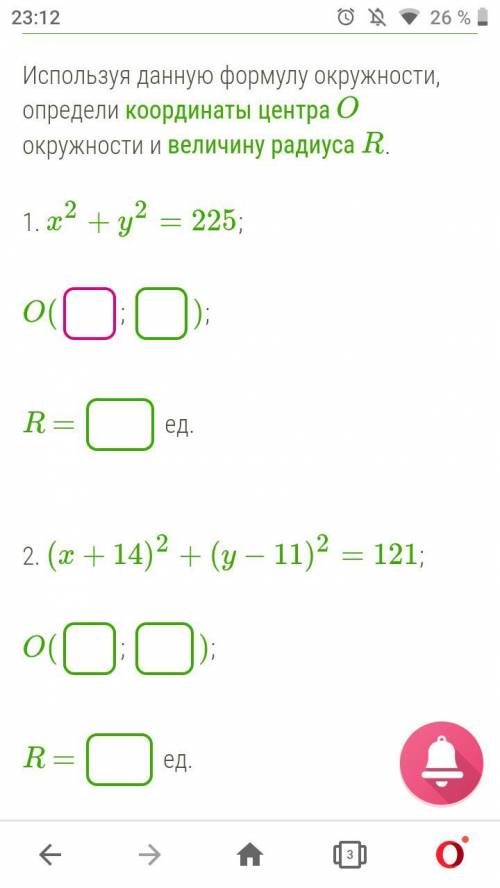
Другие вопросы по теме Геометрия
Популярные вопросы
- УМОЛЯЮ СОР ПО ЕСТЕСТВО ЗНАНИЮ 5 ЕЛАСС 2 ЧЕТВЕРТЬ...
1 - 2. Определите массу кислорода, которую можно получить при разложении 1 моль...
1 - Evolution of jobs Use the numbers to crack the code andspell the word. Then...
1 - УЧЕНИЦА купила тетради в клетку и линейку по одинаковой цене. Всего-10 штук....
3 - Как часто встречаются на циферблате часов между собой секундная, минутная и...
2 - только правильно пишите только тут надо вставить окончание в множеством и единственный...
2 - Установите соответствие между государства религией государства...
2 - Какой закон был открыт в 1785 году...
1 - Как сказать что понятие нечего не значит, Тоесть например- обязан. Как сказать...
1 - 1. Сумма протонов и нейтронов в атоме 7Li A) 4 B) 6 C) 3 D) 7 2. Элемент, атом...
2
Объяснение:
1.При добавлении или вычетании 0 сумма не меняется, соответственно: (x-0)^2+(y-0)^2=15^2
Выходит окружность(О)=(0;0) и радиус(R)=15
2. Сложение равносильно вычетанию противоположного, соответственно: (x-(-14)^2+(y-11)2=11^2
Выходит окружность (-14;11) и радиус 11
Это всё по сравнению круга. Короче в скобках должен быть минус, если его нет, то нужно сделать как во втором примере и окружность выходит те же числа что изначально в скобках, но с противоположным знаком, а радиус это корень из того что после ровно.
Уравнение окружности с центром в точке О (0; 0) и радиусом R:
(x - x₀)² + (y - y₀)² = R²
1) x² + y² = 225
x² + y² = 15²
Значит, что радиус = 15 ед.. Центр - т. О: (0;0).
2) (x + 14)² + (y - 11)² = 121
(x + 14)² + (y - 11)² = 11²
Значит, что радиус = 11 ед.. Центр - т.О: (-14; 11).
Объяснение:
Как мы находим значение точки центра и радиуса? По формуле в начале. Какие значения мы можем подставить, чтобы получить 0 вместо квадрата? В 1-м это х = 0 и у = 0, а во 2-м - это х = -14 и у = 11. Вот и эти точки являются являются координатами центра О. R = корень правой части уравнения. В первом: R = √(15²) = |15| = 15 ед.. Во втором: R = √(11²) = |11| = 11 ед.