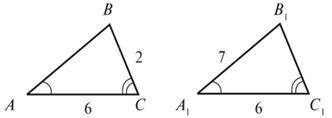
нужна с объяснениям У трикутниках ABC і A1B1C1 (див. рис.) ∠А =∠А_( 1), ∠С =∠С_( 1), AC = A1C1 = 6 см, BC = 2 см, A1В1 = 7 см. Доведіть рівність трикутників ABC і A1B1C1 і знайдіть периметр трикутника ABC.
Другие вопросы по теме Геометрия
Популярные вопросы
- Выберите верные утверждения. 1. Для плаунов характерно вегетативное размножение...
3 - Побудуйте в зошиті пряму AB.Проведіть за клітинками дві прямі, паралельні...
1 - ГАРМАТНЕ ЯДРО, МАСА ЯКОГО 10 КГ, ВИЛІТАЄ З ДУЛА ГАРМАТИ ЗІ ШВИДКІСТЮ 280М/С....
2 - Сума п яти різних натуральних чисел дорівнює 100. якого найбільшого значення...
1 - Напишите ответ на вопрос по произведению Ирины Полянской Утюжок и мороженное...
2 - (8 класс) Укажвть рівняння,що є квадратними 3x²-5x+4=0; 5x²-10x =0; 2x²+2/x=0;2x²-4x=x;...
3 - Машиною часу повісті Л.Ворониної «Таємне Товариство боягузів, або засіб...
1 - среднее арифметическое возрастов Кянана, Бабека и Эльджана равно 18. Сколько...
3 - Карточка 3 1) Найти угол BAC, если угол BOC=160°2) Найдите площадь прямоугольного...
3 - Назвати козака якого Ян Собеський називав віденським богатирем . а) | Сркоб)...
1
1. Критерий равенства треугольников:
Требуется сравнить соответствующие стороны и углы треугольников ABC и A1B1C1.
В данной задаче дано, что угол А равен углу А1, а угол С равен углу С1. Также, указано, что AC = A1C1 = 6 см и BC = 2 см, A1В1 = 7 см.
Мы можем заметить, что треугольники ABC и A1B1C1 имеют одну общую сторону AC = A1C1 и равные два угла: ∠А = ∠А1 и ∠С = ∠С1.
Теперь нам нужно сравнить соответствующие стороны треугольников. Для этого мы можем использовать теорему косинусов.
2. Теорема косинусов:
Для треугольника с известными сторонами a, b, c и противолежащим углом α, косинус угла α можно найти по следующей формуле:
cos(α) = (b^2 + c^2 - a^2) / (2bc)
Используя теорему косинусов, мы можем найти значения косинусов углов треугольников ABC и A1B1C1. Затем, сравнивая значения, мы можем доказать равенство треугольников.
Давайте посмотрим на треугольник ABC:
AB = BC = 2 см (дано)
AC = 6 см (дано)
Мы можем найти косинус угла А:
cos(A) = (BC^2 + AC^2 - AB^2) / (2BC * AC)
cos(A) = (2^2 + 6^2 - 2^2) / (2 * 2 * 6)
cos(A) = (4 + 36 - 4) / (24)
cos(A) = 36 / 24
cos(A) = 3 / 2
cos(A) = 1.5
Теперь давайте посмотрим на треугольник A1B1C1:
A1B1 = 7 см (дано)
A1C1 = AC = 6 см (дано)
Мы можем найти косинус угла А1:
cos(A1) = (A1B1^2 + A1C1^2 - B1C1^2) / (2A1B1 * A1C1)
cos(A1) = (7^2 + 6^2 - B1C1^2) / (2 * 7 * 6)
cos(A1) = (49 + 36 - B1C1^2) / (84)
cos(A1) = (85 - B1C1^2) / (84)
cos(A1) = (85 - B1C1^2) / (84)
Мы видим, что косинус угла А1 составляет 1.5, которое же значение мы получили для косинуса угла А треугольника ABC. Это означает, что углы А и А1 треугольников ABC и A1B1C1 соответственно равны.
Аналогично, мы можем применить теорему косинусов для углов С и С1 треугольников ABC и A1B1C1 и обнаружим, что косинусы этих углов также равны друг другу.
Из этого следует, что треугольники ABC и A1B1C1 равны (совпадают).
Таким образом, с учетом равенства углов и сторон, мы можем заключить, что треугольники ABC и A1B1C1 равны.
3. Найдем периметр треугольника ABC:
Периметр треугольника - это сумма длин его сторон.
ABC: AB + BC + AC = 2 + 2 + 6 = 10 см.
Таким образом, периметр треугольника ABC равен 10 см.