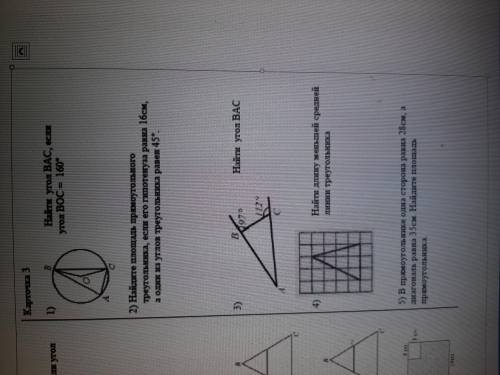
Карточка 3 1) Найти угол BAC, если угол BOC=160°

2) Найдите площадь прямоугольного треугольника (продолжение на фото)

3) Найти угол BAC

4) Найти длину меньшей средней линии треугольника

5) В прямоугольнике одна сторона равна 28см (продолжения на фото)

1) Чтобы найти угол BAC, нам необходимо использовать свойство, что сумма углов в треугольнике равна 180 градусов. Мы уже знаем, что угол BOC равен 160 градусов. Угол BAC будет равен разности между 180 градусами и суммой углов BOC и BCO.

Угол BAC = 180° - (BOC + BCO)
Угол BAC = 180° - (160° + 20°)
Угол BAC = 180° - 180°
Угол BAC = 0°

Ответ: Угол BAC равен 0 градусов.

2) Для нахождения площади прямоугольного треугольника, мы можем использовать формулу S = (1/2)*a*b, где a и b - это длины катетов треугольника. На фотографии изображен прямоугольник со сторонами 28 см и 15 см. Одна из сторон прямоугольника является основанием треугольника, а другая сторона - его высотой.

Площадь треугольника = (1/2)*28 см * 15 см
Площадь треугольника = 210 см²

Ответ: Площадь прямоугольного треугольника равна 210 см².

3) Нам уже известно, что угол BAC равен 0 градусов.

Ответ: Угол BAC равен 0 градусов.

4) Чтобы найти длину меньшей средней линии треугольника, нам нужно знать длины сторон треугольника. Однако на фотографии не указаны эти значения, поэтому мы не можем решить эту задачу на данный момент.

5) Нам дано, что одна сторона прямоугольника равна 28 см. На фотографии видно, что эта сторона является основанием треугольника. Мы также видим, что высота треугольника проходит через середину основания и образует прямой угол с ним.

Чтобы найти высоту треугольника, мы можем использовать гипотенузу и один из катетов прямоугольного треугольника по теореме Пифагора. Гипотенуза треугольника равна стороне прямоугольника, а катет равен половине стороны перпендикуляра (высоты).

a² + b² = c²
(14 см)² + (h/2)² = (28 см)²
196 см² + (h/2)² = 784 см²
(h/2)² = 588 см²
h/2 = √588 см
h = 2√588 см
h = 2 * 2√147 см
h = 4√147 см

Ответ: Высота треугольника равна 4√147 см.