найти наименьшую высоту треугольника, стороны которого равны 7 см, 8 см и 9 см​

Полупериметр тр-ка: р = 0,5(7 + 8 + 9) = 12

р-а = 12 - 7 = 5

р - в = 12 - 8 = 4

р - с = 12 - 9 = 3

Площадь тр-ка по формуле Герона:

S = √(p·(p-a)(p-в)(p-c)

S = √(12·5·4·3) = 12√5

Наименьшая высота проведена к наибольшей стороне

Ннаим = 2S:c = 2·12√5:9 = (8√5)/3

ответ: наименьшая высота равна (8√5)/3 см

(см. объяснение)

Объяснение:

Сразу замечу, что задача составлена неграмотно. Высота измеряется в сантиметрах, а не сантиметрах квадратных, поэтому правильного ответа здесь заведомо нет! Если пренебречь этой существенной неточностью, видим, что в последнем варианте не сокращена дробь, хотя .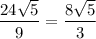

Комментарий:

Задачу можно было решить, не зная формулы Герона (хотя она есть в школьной программе).

Покажем, что достаточно уметь применять теорему Пифагора:

Решая систему, получаем, что .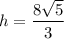

Однако такой подход, как мне кажется, менее оптимален.

Задание выполнено!