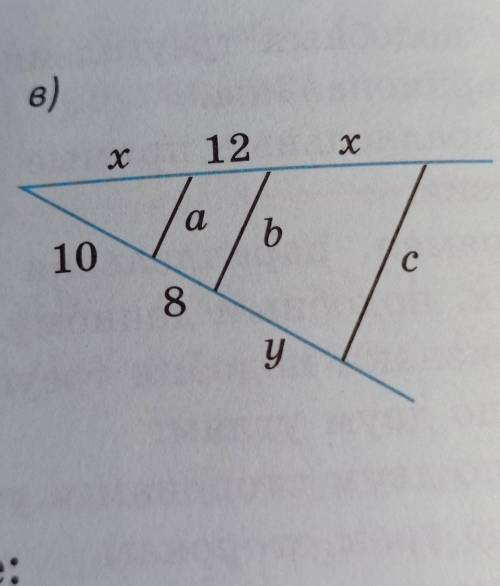
Найдите значение x+Y, если a||b||c||d​

Чтобы решить эту задачу, мы должны использовать информацию об углах и параллельных линиях.

1) Изображение показывает, что у нас есть две параллельные прямые линии, обозначенные как a и b.

2) Также есть три пересекающиеся прямые линии, обозначенные как c, d и e.

3) Мы можем использовать свойство пересекающихся и параллельных линий, чтобы найти значения углов.

4) Для начала, мы замечаем, что угол a1 и угол c1 образуют пару вертикальных углов, которые равны. Поэтому мы можем записать: a1 = c1.

5) Аналогично, угол b1 и угол d1 образуют пару вертикальных углов, которые также равны: b1 = d1.

6) Также, угол c2 и угол e1 образуют пару вертикальных углов, поэтому они равны: c2 = e1.

7) Из свойства пересекающихся прямых, мы знаем, что угол a1 и угол b1 образуют смежные углы. Сумма смежных углов равна 180 градусов. Поэтому мы можем записать: a1 + b1 = 180.

8) Также, угол c1 и угол d1 образуют смежные углы, и их сумма тоже равна 180 градусов: c1 + d1 = 180.

9) Мы также можем заметить, что угол a1 и угол d1 образуют пару вертикальных углов, поэтому они равны: a1 = d1.

10) Теперь мы можем заменить значения углов в уравнении a1 + b1 = 180: a1 + a1 = 180.

11) Производим вычисления: 2a1 = 180.

12) Делим обе части уравнения на 2, чтобы найти значение угла a1: a1 = 90.

13) Теперь мы можем найти значения углов b1, c1 и d1, используя свойства параллельных и пересекающихся прямых.

14) Так как a и b параллельны, то угол b1 и угол c2 образуют пару соответственных углов и равны между собой: b1 = c2. Следовательно, b1 = 90.

15) Также, угол c1 и угол d1 образуют пару вертикальных углов, поэтому они равны: c1 = d1 = 90.

16) Теперь мы можем найти значения углов e1 и c2. Сумма углов e1, c2 и a1 должна быть 180 градусов.

17) Заменяем значения углов: e1 + c2 + a1 = 180.

18) Подставляем известные значения: e1 + 90 + 90 = 180.

19) Выполняем вычисления: e1 = 0.

20) Итак, мы получили значения углов: a1 = 90, b1 = 90, c1 = 90, d1 = 90 и e1 = 0.

21) Теперь мы можем найти значение x + y. Обратите внимание, что угол a1 и угол c1 (или b1 и d1) образуют пару вертикальных углов, которые равны.

22) Значит, x и y должны быть равными значениями.

23) Таким образом, x + y = a1 + c1 = 90 + 90 = 180.

Итак, значение x + y равно 180.