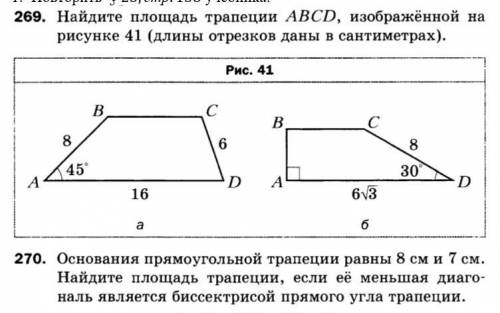
Найдите площадь трапеции ABCD, изображённой на
рисунке 41 (длины отрезков даны в сантиметрах).
Рис. 41
C
8
6
8
45°
16
D
6v3
30
270. Основания прямоугольной трапеции равны 8 см и 7 см. Найдите площадь трапеции, если её меньшая диагональ является биссектрисой прямого угла трапеции.

Привет! Давай решим задачу на нахождение площади трапеции.

У нас есть трапеция ABCD со следующими данными:
- Основания трапеции: AC (длина 8 см) и BD (длина 7 см).
- Угол ABC равен 45 градусов.
- Длина биссектрисы прямого угла трапеции равна 6√3 см.

Для решения задачи, нам понадобятся несколько шагов.

Шаг 1: Найдем высоту трапеции.
Высота трапеции - это перпендикуляр, опущенный из вершины одного из оснований на противоположное основание. В данной задаче, в качестве высоты будет выступать отрезок BC (длина неизвестна).

Шаг 2: Найдем длину отрезка BC.
Мы знаем, что основания трапеции равны и одно из них - AC - имеет длину 8 см. Также мы знаем, что угол ABC равен 45 градусам. У нас есть основание AC, угол ABC и искомая сторона BC, поэтому мы можем использовать тригонометрию для нахождения длины отрезка BC.

Так как угол ABC равен 45 градусам, тогда угол BAC (около основания AC) равен 90 - 45 = 45 градусам.

Теперь мы можем использовать тангенс угла для нахождения отношения длин сторон прямоугольного треугольника BAC:

тангенс угла BAC = BC / AC.

Тангенс угла 45 градусов равен 1 (так как тангенс 45 градусов равен 1), поэтому у нас получается следующее уравнение:

1 = BC / 8.

Отсюда мы можем найти длину отрезка BC:

BC = 8 см.

Шаг 3: Найдем площадь трапеции.
Трапеция - это фигура, которая состоит из двух параллельных оснований и высоты, опущенной на основание. Площадь трапеции можно найти, используя следующую формулу:

Площадь трапеции = (сумма оснований) * (высота) / 2.

В нашем случае, основания трапеции равны 8 см и 7 см, а высота равна 6√3 см, поэтому мы можем вычислить площадь:

Площадь трапеции = (8 + 7) * 6√3 / 2.

Площадь трапеции = 15 * 6√3 / 2.

Площадь трапеции = 45√3 / 2.

Итак, площадь трапеции ABCD составляет 22.5√3 квадратных сантиметров.

Надеюсь, я смог объяснить решение задачи и ответить на твой вопрос. Если у тебя есть еще вопросы, не стесняйся задавать!