1. Геометрия
  2. Найдите площадь ромба, высота

Найдите площадь ромба, высота которого равна (120 √41)/41 и его диагонали относятся как 4:5

alinadudocka alinadudocka    3   06.03.2022 15:01    2

Ответы
ЛенаКошка ЛенаКошка  06.03.2022 15:10

\boxed{S_{ABCD} = 360} квадратных единиц

Объяснение:

Дано: BK = \dfrac{120\sqrt{41} }{41} , BK \perp AD, BD : AC = 4 : 5

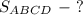
Найти: S_{ABCD} \ - \ ?

Пусть BD ∩ AC = O.

Так как по условию BD : AC = 4 : 5, то введем коэффициент пропорциональности x, тогда BD = 4x, AC = 5x.

По свойствам ромба его диагонали точкой пересечения делятся пополам, тогда AO = OC = AC : 2 = 5x : 2 = 2,5x; BO = OD = 4x : 2 = 2x.

Так как по свойствам ромба AC ⊥ BD, то по теореме Пифагора для треугольника ΔAOD: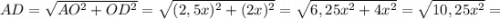 AD = \sqrt{AO^{2} + OD^{2}} = \sqrt{(2,5x)^{2} + (2x)^{2}} = \sqrt{6,25x^{2} + 4x^{2} }=\sqrt{10,25x^{2} } =

= x\sqrt{10,25} .

Запишем систему уравнений выразив площадь ромба:

\displaystyle \left \{ {{S_{ABCD} = BK \cdot AD } \atop { S_{ABCD} = 0,5 \cdot AC \cdot BD }} \right \Longrightarrow \boxed{ BK \cdot AD = 0,5 \cdot AC \cdot BD}

BK \cdot AD = AC \cdot BD

\dfrac{120\sqrt{41} }{41} \cdot x\sqrt{10,25} = 0,5 \cdot 4x \cdot 5x|:x

10x = \dfrac{120 \cdot 20,5}{41}|:10

x = \dfrac{12 \cdot 20,5}{41} = \dfrac{246}{41} = 6

\boxed{S_{ABCD} = 0,5 \cdot AC \cdot BD = 0,5 \cdot 5x \cdot 4x = 10x^{2} = 20 \cdot 6^{2} = 10 \cdot 36 = 360} квадратных единиц.


Найдите площадь ромба, высота которого равна (120 √41)/41 и его диагонали относятся как 4:5
ПОКАЗАТЬ ОТВЕТЫ
яглупенькая яглупенькая  06.03.2022 15:10

360

Объяснение:


Найдите площадь ромба, высота которого равна (120 √41)/41 и его диагонали относятся как 4:5
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
LLarь LLarь  20.01.2021 06:21
Можете быстро тут нужно назвать углы. Зарание...
NikaMalinka2 NikaMalinka2  20.01.2021 06:23
По данным на чертеже найти длину отрезка km​...
tamtamtamira tamtamtamira  05.02.2022 19:34
Определите вид ушла М треугольника МТС...
kazorinJeka kazorinJeka  05.02.2022 19:33
Бісектриса трикутника ділить сторону на відрізки, різниця яких 1 см. Знайдіть периметр трикутника,якщо дві інші його сторони 10 і 8 см...
ailchencko2010 ailchencko2010  05.02.2022 19:32
На рисунке AB : AD = AC : AE = BC : ED. Это означает, что угол ABC подобен ... и угол ABC = углу ...; угол ВСА = углу ......
kektuber222owf6bv kektuber222owf6bv  05.02.2022 19:28
Основи ривнобичнои трапеции доривнують 16см та 40 см.Бични сторони доривнують по 20 см.Знайдить висоту....
McVano McVano  05.02.2022 19:23
найти углы равнобедреннного треугольника, если угол при основании на 36⁰ больше угла при вершине равнобедреннного треугольника...
mozhnj mozhnj  05.02.2022 19:21
найди площядь пересечения окружностей (ВЫДЕЛИНУЮ СТОРОНУ) это 2 одинаковых окружности...
you58 you58  05.02.2022 19:19
Бічна сторона рівнобедреного трикутника на 1см більша за основу. Знайдіть радіус вписаного кола, якщо периметр трикутника дорівнює 50см...
Oleg12875 Oleg12875  06.10.2019 20:28
Диагонали ac и bd четырёхугольника abcd, вписанного в окруж-ность, пересекаются в точке к. найдите длину отрезка ак, если ab = 15,cd = 10, ac = 20, bd = 16.​...

Популярные вопросы