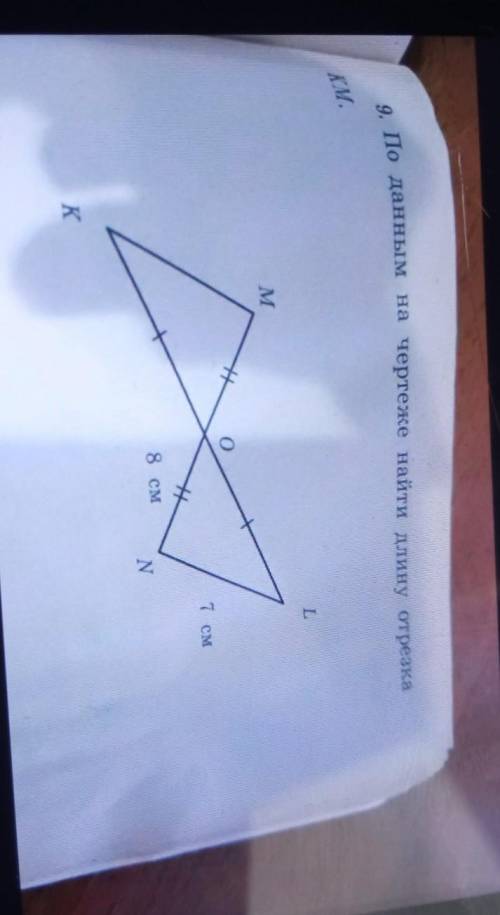
По данным на чертеже найти длину отрезка km​

тоже 7

треугольники равны по 2 сторонам и углу между ними

Для нахождения длины отрезка km на данном чертеже мы можем использовать теорему Пифагора. Эта теорема говорит нам, что в прямоугольном треугольнике квадрат длины гипотенузы (в данном случае отрезка km) равен сумме квадратов длин катетов (в данном случае отрезков kl и lm).

Шаг 1: Найдем длину отрезка kl.
На чертеже можно заметить, что отрезок kl вертикальный и параллелен одной из сторон прямоугольного треугольника. Это означает, что отрезок kl является катетом прямоугольного треугольника.

Шаг 2: Измерим длину отрезка kl.
На чертеже мы видим, что длина отрезка kl равна 6,5 см.

Шаг 3: Найдем длину отрезка lm.
Отрезок lm является горизонтальной стороной прямоугольного треугольника и также является катетом.

Шаг 4: Измерим длину отрезка lm.
На чертеже мы видим, что длина отрезка lm равна 9 см.

Шаг 5: Используем теорему Пифагора для нахождения длины отрезка km.
Согласно теореме Пифагора, квадрат длины отрезка km равен сумме квадратов длин отрезков kl и lm.

В данном случае:
длина отрезка kl = 6,5 см;
длина отрезка lm = 9 см.

Используя теорему Пифагора, мы можем написать уравнение:
(длина отрезка km)^2 = (длина отрезка kl)^2 + (длина отрезка lm)^2.

Подставим известные значения:
(длина отрезка km)^2 = (6,5 см)^2 + (9 см)^2.

Решаем это уравнение:
(длина отрезка km)^2 = 42,25 см^2 + 81 см^2.
(длина отрезка km)^2 = 123,25 см^2.

Шаг 6: Найдем квадратный корень из результата.
Чтобы найти длину отрезка km, нужно извлечь квадратный корень из полученного результата.

Корень из 123,25 ≈ 11,09 см.

Таким образом, длина отрезка km на чертеже составляет примерно 11,09 см.