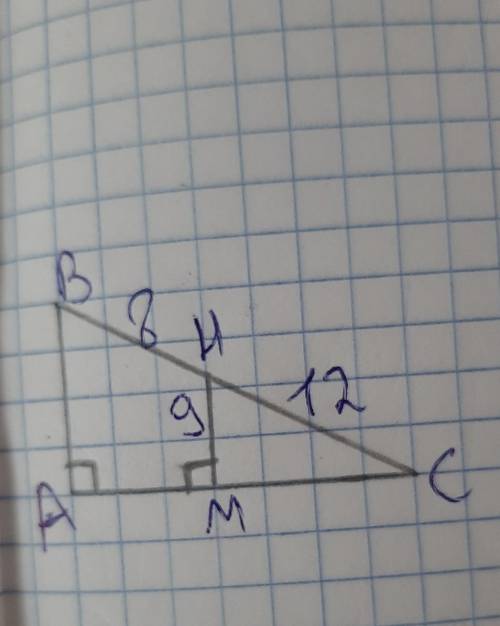
Найдите катет BA треугольника изображенного на рисунке​

Баллонов о год. Ар. О па др с шш вас на шык шш п

Хорошо, давайте решим эту задачу пошагово.

На рисунке представлен прямоугольный треугольник, где A, B и C - вершины, а BC - гипотенуза. Нам нужно найти катет BA.

Первым шагом нам нужно определить более подробно треугольник. Для этого воспользуемся теоремой Пифагора, которая гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

В данном случае у нас имеется катет BC. Пусть x - длина катета BA. Тогда согласно теореме Пифагора, мы можем записать:

BC² = AB² + AC²

Теперь нам нужно найти значения AB и AC. Обратимся к рисунку. Мы видим, что вершина А треугольника является прямым углом. Это означает, что треугольник BAC является прямоугольным.

Таким образом, мы можем использовать ту же теорему Пифагора, чтобы найти значения AB и AC.

AB² = BC² - AC²
AB² = 9² - 5²
AB² = 81 - 25
AB² = 56

Отсюда следует, что AB = √56.

Теперь, с помощью найденного значения AB, мы можем решить исходную задачу. У нас есть следующее уравнение:

BC² = AB² + AC²

Подставим значения:

10² = (√56)² + AC²
100 = 56 + AC²

Теперь решим это уравнение:

AC² = 100 - 56
AC² = 44

Отсюда следует, что AC = √44.

Итак, мы нашли длины сторон AB и AC. Теперь, вернемся к вопросу, который был задан в начале: "Найдите катет BA треугольника изображенного на рисунке". Мы решили задачу и соединили ее с исходным рисунком, поэтому у нас есть ответ: длина катета BA равна √56.